Essai d'analyses didactiques-statistiques
de la structure de l'évaluation.
Cas du cycle du lycée au Maroc

Said Haouassia, El Mostapha El khouzai
 

Résumé
Au cours de notre recherche, nous nous sommes intéressés aux structures de l'évaluation instituées par le curriculum officiel, et par conséquent aux pratiques et aux modes d'évaluation réelle.

À cet fin, nous avons fait usage d'une analyse statistique des scores des élèves au baccalauréat, en se basant sur le profil d'entrée au lycée détecté au cours de notre recherche, pour l'exploiter en tant qu'outil de dévoilement de la structure réelle de l'évaluation, pour déterminer l'écart éventuel entre cette structure et celle déclarée officiellement par le curriculum officiel comme première étape, pour élaborer une analyse didactique qui vise l'explication des causes de l'écart observé ainsi que les scores faibles des élèves dans les évaluations internationales – TIMS en particulier – des élèves d'un échantillon choisi par hasard.

Au cours de notre analyse, nous avons essayé de relater la corrélation des scores obtenus par les élèves d'une part et, d'autre part, quelques éléments d'analyse didactique à partir du cadre de la théorie de situation et le statut d'un objet en liaison avec la notion de compétence comme élément central dans le curriculum officiel.

Tous nos essais d'analyse de différentes situations d'évaluation s'inscrivent dans une vision socio-constructiviste de l'enseignement et l'apprentissage.

Notre but : d'une part, élucider la structure officielle de l'évaluation en essayant de préciser ses caractéristiques à partir d'un référentiel didactique, et d'autre part, par l'usage d'une analyse comparative entre l'évaluation officielle et les pratiques évaluatives réelles, dégager les ajustements qui s'imposent dans une vision socio-constructiviste de l'enseignement et de l'apprentissage.

Mots clés : statistique, didactique, curriculum, structure, situation.

Introduction

   Notre article se place dans le cadre d'une recherche qui s'intéresse à l'étude des effets d'un système d'évaluation à caractère standard et statique sur l'enseignement, considérant le cas de l'évaluation. Elle agit de façon croissante sur le système éducatif, sur son organisation, les programmes, les contenus, les tâches proposées, et par conséquence sur les pratiques d'enseignement, ainsi que les pratiques d'évaluation et d'orientation.

   Suite aux scores faibles des élèves marocains enregistrés dans les évaluations internationales de TIMS en particulier en 2012, nous avons entamé, dans le cadre de notre recherche, une étude qui se base sur les scores des élèves de la 3 année collège, avec l'hypothèse de les suivre jusqu'à l'année 2015, année d'arrivée de notre population de recherche au baccalauréat.

   Le présent article retrace les scores des élèves au baccalauréat de l'année 2015, en présentant une analyse statistique servant d'outil pour réaliser une analyse didactique visant la clarification de la structure officielle de l'évaluation ; et en élucidant la structure de l'évaluation réelle, dans le but de mettre en relief l'écart qui existe entre les deux d'une part ; et relater un essai didactique basé sur la théorie de situation de G. Brousseau [1] et la notion d'objet d'un concept, pour expliquer les causes de l'écart observé entre le curriculum officiel et le curriculum réel.

Éléments de problématique

Le choix des scores des élèves comme indicateur d'écart

   Nous sommes partis du fait que, parmi les rôles de l'évaluation, il y a la mesure implicite de la réalisation du curriculum officiel ainsi que la détermination du profil des élèves/étudiants à la sortie d'un cycle d'enseignement.

   Les scores des élèves-étudiants , en plus de leurs rôles de détermination de la réussite-échec d'un élève-étudiant, peuvent être un indicateur de détermination d'écart éventuel entre le curriculum réel et celui officiel, sur le plan de la structure de l'évaluation elle-même, c'est-à-dire la validité ainsi que la fiabilité de l'outil de mesure des compétences des élèves-étudiants, ainsi que sur le plan de la pratique enseignante.

Au cours de notre recherche, pendant une période de cinq ans, nous avons constaté un écart significatif entre les scores internes de l'évaluation (contrôle continu, examen local/ régional, examen national) dans les cycles du collège et du lycée, ainsi que la faiblesse des scores des élèves marocains dans les évaluations internationales – TIMS pour notre cas. Notre article se place donc dans ces préoccupations, et essaiera de relater une analyse statistique-didactique des scores des élèves du baccalauréat (nous renvoyons le lecteur au résultat de l'analyse statistique-didactique des scores des élèves au collège) en se basant sur ce que nous avons réalisé au cycle du collège en considérant ses résultats comme étant le profil d'entrée au cycle du lycée.

Sur les traces officielles, nous soulignons les points suivants : le cadre de référence de l'évaluation – cas des mathématiques pour illustration –, les circulaires organisant les contrôles continus et l'examen régional qui a pour but de :

• Dévoiler la structure de l'évaluation.

• Vérifier sa cohérence interne, et le caractère de continuité dans les cycles.

• L'évaluation en tant que mesure de compétences et de connaissances acquises de la part des élèves-étudiants au cours et la fin d'un cycle souffre de plusieurs maux :

• Compte tenu de la quantité de connaissances que doit véhiculer le programme, on constate que dans la pratique enseignante la formation scientifique est conçue dans une logique de connaissance cumulative plutôt que de répertoire de compétences telles que « savoir se construire une représentation, savoir prendre une décision, savoir argumenter ».

• Le manque de sens pour les élèves qu'ont certains cours de mathématiques. L'architecture du programme, illustré dans les manuels scolaires, est souvent davantage centrée sur des techniques et algorithmes, vus comme fin demandée par le mode d'évaluation réel.

• Le problème de la formation des enseignants : une formation des enseignants sur les différentes approches de l'évaluation est une nécessité : « devenir enseignant, c'est adopter un type de rapport au savoir et se forger une épistémologie personnelle qui inspirera tous les actes de l'enseignement » [2].

• L'état d'échec constaté à travers les résultats des élèves marocains dans les évaluations internationales – cas de TIMS – ainsi que les écarts observés entre les scores des élèves dans l'évaluation interne au niveau du système d'enseignement malgré les efforts fournis par les autorités éducatives à travers les tentatives de plusieurs réformes – la charte nationale de l'éducation et formation de l'an 2000, ainsi que le plan d'urgence en 2013, et les projets lancés (pendant notre recherche qui a débuté en 2012) en 2015 pour revoir le passage des élèves d'un niveau à l'autre en respectant la moyenne de 10/20 au collège et au lycée, et 5/10 au cycle primaire.

• Toutes les données ci-dessus justifient notre recherche et lui permettent d'apporter des éléments de réponses à caractère scientifique et didactique pour le sujet d'évaluation.

Notre hypothèse est la suivante :

   Avoir une structure interne de l'évaluation des compétences ayant une caractéristique uniforme, et des pondérations qui tiennent compte du temps d'enseignement, peut améliorer l'écart entre le curriculum officiel et le réel.

Nos questions sont les suivantes :

1. est-ce que la structure de l'évaluation actuelle des connaissances permet la mesure du profil de sortie du cycle du lycée ?

2. quel apport d'une réflexion didactique sur l'évaluation peut-il apporter à l'élucidation de ses contraintes ?

3. peut-on déterminer les causes de l'échec observé à partir des scores des élèves à la fin du cycle du lycée ?

1. Cadre théorique

   Comme nous l'avons déclaré en introduction, nous adoptons la théorie de situation de Guy Brousseau. « La théorie des situations comporte donc deux objectifs, d'une part l'étude de la consistance des objets et de leurs propriétés (logiques, mathématiques, ergonomiques), nécessaires à la construction logique et à l'invention de "situations", et d'autre part la confrontation scientifique (empirique ou expérimentale) de l'adaptation de ces modèles et de leurs caractéristiques avec la contingence » . De plus, « une situation modélise les enjeux et les possibilités de décision d'un actant dans un certain milieu. Elle est choisie de telle manière que la stratégie de résolution ne puisse être mise en œuvre que grâce à une certaine connaissance mathématique, l'apparition de cette décision sans l'usage par l'actant de la connaissance visée étant hautement improbable ». Dans notre cas, les décisions prises par l'intermédiaire des scores de l'évaluation par le système éducatif concernant la réussite-l'échec d'un élève-étudiant, basées sur sa performance et son acquisition des connaissances-compétences, subissent des stratégies implicites au cours du cycle pour devenir explicites à la fin du cycle. Dans une correspondance sur le sujet, Brousseau m' a fait savoir que la théorie de situation n'a pas abordé le sujet d'évaluation, vu sa complexité, et qu'il reste à le compléter par de telles réflexions. « C'est en fait le sujet le plus complexe, le plus important et le plus désolant que j'ai rencontré tant j'y vois d'erreurs et d'obstacles.
Par exemple pour comprendre les échecs répétés (récursifs) des tentatives de réformes initiées par des administrations guidées par des principes de management totalement ignorants de la complexité des phénomènes, il faut conjuguer des observations et des approches théoriques de phénomènes très différents : le fonctionnement des connaissances et des références (savoirs) dans le travail des élèves, la façon dont les professeurs essaient de maintenir un équilibre entre les deux par le choix des situations proposées et de leurs enseignements, par la façon dont ils répondent aux difficultés des élèves, dont ils réagissent aux échecs, la façon dont ils réagissent aux objurgations de leur hiérarchie, lesquelles accentuent leurs difficultés et aboutissent à des excès incontrôlables » [3].

2. Méthodologie et analyse des scores des élèves

   Notre recherche vise à rendre explicites les méthodes d'analyse statistique des scores des élèves, et à ne pas les réduire à une simple lecture descriptve basée sur le paramètre de moyenne, afin de pousser l'étude à l'élucidation de rapports possibles entre les éléments qui constituent la moyenne, à savoir les rapports pondérés sur l'acquisition des divers savoirs évalués, et à dresser un essai d'analyse didactique sur la structure d'évaluation des acquis cognitifs.

   Nous croyons qu'une approche statistique s'inscrivant dans une approche didactique à partir de la théorie des situations et de la signification d'un objet en terme de sens est susceptible d'ouvrir de nouvelles pistes de recherche dans le sujet de l'évaluation qui demeure vierge au niveau des évaluations internes des systèmes éducatifs y compris le cas du Maroc.

   Le repérage de la structure de l'évaluation interne, à savoir : le contrôle continu, l'examen local et régional ainsi que l'examen national.

   Notre choix de méthodes s'est fixé sur les outils suivants :

• Scores d'un échantillon choisi au hasard de taille 42 000 élèves au baccalauréat en 2015.
• Analyse statistique.
• Analyse didactique des scores.

   La phase I consiste à présenter les données descriptives de notre échantillon.

   Ce choix repose d'abord sur les trois traits distincts de l'évaluation interne : examen régional, examen national, et par déduction les contrôles continus.

   Ces caractéristiques sont nécessaires pour pouvoir déterminer le degré de liaison entre les scores des matières évaluées, et en déduire des éléments de réponses sur la nature de corrélation entre les scores, et essayer d'expliquer didactiquement les causes de ces corrélations éventuelles.

   La phase II consiste à formuler une analyse didactique à partir du cadre théorique adopté ci-dessus (théorie de situations et sens d'un objet).

3. Les données descriptives du premier échantillon

3.1. Nous tenons tout d'abord à rappeler que le présent article retrace une étape de notre recherche qui a concerné les cycles du système éducatif : collège, lycée et supérieur ; nous avons poursuivi notre échantillon à partir du collège qui était d'une taille de 4 623 élèves, pour l'agrandir à 42 000 élèves au lycée pour qu'il soit représentatif.

3.2. Rappel des conclusions concernant le cycle du collège

   L'écart observé entre le curriculum réel et celui officiel se présente comme suit :

• Le contrôle continu représente 60 % de la moyenne annuelle au lieu de 30 % décrété par les orientations officielles, dont les matières d'éveil comptent pour 34 %.

• L'examen local normalisé représente 27 % de la moyenne annuelle au lieu de 30 %, poids accordé par la note ministérielle n° 43.

• L'examen régional normalisé ne représente que 13 % du poids afférent à la décision au lieu de 40 % arrêté par les autorités éducatives.

• Moins de 70 % des élèves du public ont un profil littéraire et seuls 20 % ont un profil scientifique.

• Par contre pour le privé, le profil scientifique est réalisé chez 60 % des élèves et le profil littéraire chez 70 %.

• Presque 60 % de ceux qui sont orientés en sciences ont réalisé de bonnes performances en lettres. Plus de73 % de ceux qui sont orientés en lettres ont un seuil littéraire inférieur à la moyenne théorique. Le seuil de réussite de 08/20 leur a donné accès au cycle qualifiant malgré leurs lacunes.

• Seuls 2,5 % des élèves orientés en lettres ont un profil scientifique

• 38,5 % des élèves orientés en sciences ont vraiment un profil scientifique [4].

   Les données ci-dessus nous informent sur le profil d'entrée au cycle du lycée, tout en remarquant que 61,5 % des élèves orientés dans les branches scientifiques n'ont pas le profil demandé par le curriculum officiel.

   La suite de notre article prendra le profil détecté chez les élèves du collège comme le profil réel d'entrée au lycée, comme postulat de départ, pour ensuite retracer le mouvement de ce profil selon les scores réalisés à la fin du cycle du lycée.

3.3. Présentation descriptive des données de l'échantillon

   Pour situer nos données descriptives, on remarque que le cadre de référence de l'évaluation des acquis marocain pour la certification du baccalauréat, privilégie la mesure des connaissances et savoirs, comme c'est le cas pour le TIMS, donnée qui peut justifié le choix de la participation du Maroc à l'évaluation international d'IAE, avec l'observation de son obstination à participer dans les évaluations de terminale de TIMS.

   Comme nous pouvons remarquer l'octroi de 50 % [5] pour les applications directes des algorithmes et techniques, quand au niveau C il n'y a que 15 %, cette chose nous pousse à poser la question du statut de la compétence comme étant une mobilisation des « ressources, savoirs et connaissances » dans des situations « d'intégration » ou de connexion des cadres au sens de R. Douady [6].

   Pour les 35 % qui restent, on peut postuler que l'architecture de l'évaluation prévoit des situations dont la formulation serait une variable déterminante, mais dans ce cas, nous constatons qu'il y a un vieillissement des situations d'évaluation, qui rend la réforme prévue non réalisable du fait des situations proposées durant une décennie depuis l'adoption des cadres de référence, des situations familières (et glisse au niveau), avec « la tolérance » acceptée pour le niveau C.

   Théoriquement cela suppose l'obtention de scores élevés de la part des élèves, mais tenant compte du profil d'entrée des individus de notre échantillon dont 61,5 % n'a pas le profil scientifique et poursuit une formation dans des branches scientifiques, cela nous poussera à poser les questions suivantes : est-ce que la structure de l'évaluation officielle permettra de réguler une telle déformation ? est-ce que l'on obtiendra les mêmes écarts entre les structures de l'évaluation ?

Pour ce faire, nous allons exposer les premiers résultats :

Statistiques descriptives

   Nous constatons que la moyenne observée en mathématiques n'atteint pas la moyenne, c'est-à-dire que ce paramètre nous indique que le niveau A prévu n'est pas atteint par la population, de même pour la physique et les SVT, ainsi que les langues : arabe, français et anglais. Tenant compte du fait que le score d'entrée au lycée était en moyenne de 8/20, nous constatons que les scores moyens de toutes les matières sont voisins de cette moyenne. De plus, les moyennes constatées pour les disciplines littéraires ont tendance à dépasser celles des matières scientifiques.

   S'agissant du paramètre de la moyenne, cela nous poussera à utiliser d'autres paramètres comme l'écart-type car il a la même dimension que la moyenne, pour avoir plus de visibilité sur la dispersion des scores de notre échantillon.

Statistiques descriptives

   Les statistiques du tableau ci-dessus montrent que la moyenne en mathématiques est de 8,56. Cette note loin de la moyenne attendue (10) indique, malgré la présence de notes assez élevées chez certains élèves, que le nombre d'élèves ayant des notes assez faibles est très élevé. L'écart-type de cette série de notes est égal à 5,88. Cette valeur élevée indique qu'une note prise au hasard peut être loin de la moyenne de 5,88, et que les notes sont concentrées dans l'intervalle [moyenne – l'écart type, moyenne + l'écart type], c'est-à-dire qu'il y a certains élèves de l'échantillon qui ont des bonnes compétences en mathématiques, alors que d'autres soufrent de beaucoup de difficultés en mathématiques. Cela peut être expliqué par le pourcentage des élèves orientés en branches scientifique selon le profil d'entrée au cycle du lycée (38,5 % des élèves orientés en sciences ont vraiment un profil scientifique). De plus, l'écart-type peut être un indicateur de la non-régulation des pratiques d'évaluation surtout dans les dimensions : contrôles continus et examen régional, puisque elles sont conçues selon le curriculum officiel pour cette mission, en tenant compte a priori du rôle diagnostique et formatif de l'évaluation. La pratique réelle de l'évaluation n'a pas réussi à minimiser le caractère hétérogène du profil des élèves au cycle du lycée.

   Au contraire nous constatons que le profil d'entrée au cycle lycée est toujours présent à la phase certificative, ce qui justifie notre question globale de la recherche sur les profils de sortie de chaque cycle : collège, lycée, supérieur ; et en conséquence le rendement du système éducatif en termes d'acquisitions de compétences.

   Pour les autres matières, à savoir les sciences physiques, les sciences de la vie et de la terre et le français (physique ; sciences de la vie et la terre ; anglais), on constate que les moyennes observées sont plus faibles (6,03 ; 7,49 ; 7,93). Cela indique que le nombre d'élèves ayant des difficultés augmente mais les niveaux de difficultés chez les élèves pour la maîtrise de ces matières se rapprochent. Les écarts entre les niveaux se réduisent par rapport à ceux observés en mathématiques (4,53 ; 4,58 ; 4,93).

   Concernant les langues arabe et anglaise, les moyennes sont de l'ordre de 9,24 et 9,79. Ces valeurs montrent que pour ces deux matières, les niveaux d'élèves sont meilleurs ; mais les écarts restent importants (pour l'anglais écart-type = 4,65 pour et pour l'arabe l'écart-type est de 3,40.

   Cela confirme le constat que toutes ces matières ont une moyenne inférieure à 10.

   Pour pousser la réflexion, on peut se poser la question du degré du lien entre les matières, autrement dit le degré d'influence d'une matières sur l'autre, partant du fait que les mathématiques par exemple sont véhiculés par « le dialecte » en classe, rédigé en arabe, avec un symbolisme d'origine latine « dans lequel on trouve le français et l'anglais ». Ce multilinguisme incorporé dans le cours de mathématiques détruit complètement le sens.

   Nous avons conçu une matrice de corrélation pour avoir plus de visibilité.

Matrice de corrélation

   Le tableau ci-dessus présente les corrélations existant entre les différents couples avec un niveau de signification de 1 % (et un niveau de confiance de 99 %).

   L'analyse de ces résultats (matrice de corrélation) montre que les différentes valeurs du coefficient de corrélation sont positives, cela indiquant l'existence d'une corrélation positive entre les différentes matières. Toutefois l'intensité de ces corrélations diffère d'un couple de variables (matières) à l'autre. Les variables mathématiques et physique sont fortement corrélées (r = 0,786). Cela suggère que plus la note des mathématiques augmente, plus la note de physique augmente, et vice-versa ; les élèves ayant un bon niveau en mathématiques, l'ont aussi en physique. Les mêmes constatations sont observées entre les mathématiques et les sciences de la vie et la terre ; sciences de la vie et la Terre-physique. Par contre, les corrélations entre les mathématiques et les langues sont moyennes et positives : mathématiques-français (r = 0,46) et mathématiques-anglais (r = 0,51). mathématiques-arabe (r = 0,465). Cela suggère qu'un niveau moyen dans les langues peut être suffisant pour avoir un bon niveau en mathématiques et physique. En revanche, l'influence des langues devient notable pour la maîtrise des sciences de la vie et de la terre. En ce sens nous constatons que la structure d'orientation officielle, qui est censée prendre ses décisions à partir des profils des élèves a tendance à orienter les élèves dont le profil de maîtrise des langues est faible vers la branche des sciences de la vie et la terre !

   Au niveau des langues, on constate que le français et l'anglais sont fortement corrélés. Ainsi les élèves ayant un bon niveau en langue française ont-ils un bon niveau en anglais et vice- versa. Même si leur niveau en arabe est moyen.

   Nous présentons ci-dessous un tableau de répartition des scores (notes) des élèves dans les matières d'évaluation.

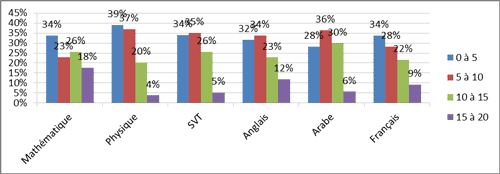
   Pour ensuite présenter les distributions marginales pour chaque matière, ainsi que les répartitions des scores.

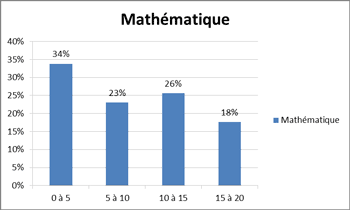
   Si nous prenons en compte le fait que les mathématiques figurent dans tous les programmes et le curriculum des branches scientifiques et économiques dans le cycle supérieur, la répartition marginale des mathématiques nous informe du caractère continu du profil d'entrée au cycle du lycée, à savoir que 44 % de l'échantillon a la moyenne espérée, dont 26 % satisfait le niveau A des cadres de référence d'examen national et 18 % seulement sont dans les niveaux dans B et C.

   Si on le compare au fait que 38 % de l'échantillon avait un profil scientifique comme profil d'entrée au lycée, nous remarquons qu'il y a une amélioration de 6 % pour ce constituant, mais il reste à vérifier le statut du sens d'un objet mathématique, surtout lorsque il est utilisé comme outil de modélisation des problèmes physiques, sans oublier que la moyenne observée de la physique est de 6,03.

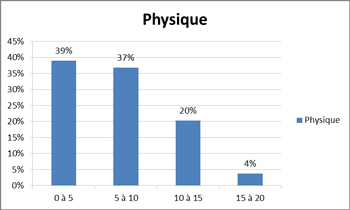
   Nous constatons dans la répartition marginale de la physique que seulement 24 % de l'échantillon a atteint la moyenne de 10/20 et que seulement 4 % a pu atteindre le niveau C, niveau qui appelle à la synthèse, autrement dit incite à utiliser l'objet mathématique en tant qu'outil de résolution de problèmes.

   Quant aux sciences de la vie et de la terre leur répartition nous informe que :

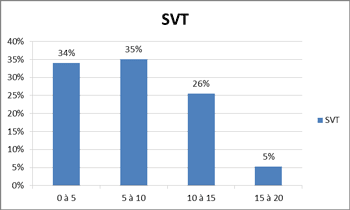
   31 % ont obtenu la moyenne, tandis que 5 % figurent dans le niveau C ; en tenant compte des corrélations mentionnées ci-dessus, concernant le lien des langues et la maîtrise des matières scientifiques, nous constatons que l'influence est très ressentie dans les sciences de la vie et de la terre.

4. Essai d'analyse didactique

   Nous allons dans un premier temps présenter un cas du cadre de référence d'évaluation – cas des mathématiques, de la branche sciences expérimentales – [5 bis], pour ensuite l'analyser à partir de la taxonomie de R. Gras [7] (R. Gras qui fait partie de l'école de Brousseau).

   Nous tenons à signaler que la conception officielle conçoit les cadres de références des examens certificatifs comme suit [8].

   Cette conception est consciente du fait que les cadres de références sont l'outil de mesure d'acquisition de connaissances et de compétences prévus par les programmes scolaires, sans pour autant déclarer qu'il jouera le rôle de régulation des écarts possibles entre la pratique enseignante et l'architecture adoptée par les programmes (dans les manuels scolaires en vigueur ou sur les modèles des sujets d'examens d'évaluation certificative dont on constate qu'ils suivent un modèle analogique dans sa phase primaire [9], c'est-à-dire que les sujets proposés pendant une décennie sont semblables dans la formulation des énoncés, mesurent les mêmes techniques et algorithmes dans la même forme sans pour autant utiliser une variable didactique dans les formes et la formulation) pour véhiculer les compétences qui constituent les profils recherchés dans le curriculum officiel.

4.1. Cadre de référence des mathématiques

Tableaux de spécification.

A suivant les domaines principaux.

B suivant les niveaux d'habilités.

   Nous constatons que la répartition de la pondération officielle réserve la moitié de la note globale aux applications directes des connaissances enseignées ce que nous avons désigné dans cet article par le niveau A. Quant à B, il consacre 35 % pour le paramètre de la formulation implicite dans l'énoncé prévu pour l'examen, tout en gardant l'aspect routinier de la situation d'évaluation, et consacre 15 % pour les situations de synthèse.

   Tenant compte des répartitions des notes des mathématiques par exemple, nous trouvons que 82 % de l'échantillon n'atteint pas le niveau C, sachant que la moyenne est de 8,56 et l'écart- type est de 5,88. Cela suppose que même les élèves qui dépassent 15 n'atteignent pas le niveau C.

   Ce résultat confirme l'appropriation de l'échantillon des connaissances algorithmiques directes avec des difficultés remarquables une fois que l'énoncé du sujet opère une variation didactique au niveau de la formulation des questions. Pour approfondir l'analyse du cadre de référence et pouvoir comparer nos résultats escomptés avec le point de départ de nos questions de recherche. Afin d'élaborer quelques éléments de réponses qui tiennent compte d'une comparaison des résultats des élèves de l'échantillon aux résultats de TIMS [10], nous allons adopter la taxonomie de R. Gras d'objectifs cognitifs qui est une taxonomie spécialement établie et validée pour les mathématique. De plus son auteur adhère à notre cadre théorique. Cela nous servira d'outil pour approcher le cadre de TIMS.

Taxonomie de R. GRAS

   Pour le niveau A1 de Gras, à savoir connaître la terminologie du fait spécifique. Du fait du multilinguisme « dialecte, arabe, véhiculé explicitement : le premier dans la phase orale et le deuxième dans la phase écrite, ainsi que le français et l'anglais implicitement par la présence des symboles latins dans l'institutionnalisation du savoir mathématique » observé dans la pratique enseignante des mathématiques, le terme connaissance que Guy. Brousseau définit ainsi : « l'élève produit ses connaissances comme réponse personnelle à une question et les fait fonctionner ou les modifie comme réponses aux exigences du milieu et non à un désir du maître. La différence est grande entre s'adapter à un problème que le milieu vous pose, incontournable, et s'adapter au désir du professeur : la signification de la connaissance est complètement différente ; une situation d'apprentissage est une situation dans laquelle ce qu'on fait a un caractère de nécessité par rapport à des obligations qui ne sont pas arbitraires, ni didactiques. Or toute situation didactique contient une part d'intention et de désir de la part du maître ». De plus, « notons qu'il ne suffit pas de "communiquer" un problème à un élève pour que ce problème devienne son problème et qu'il se sente seul responsable de le résoudre. Il ne suffit pas non plus que l'élève accepte cette responsabilité pour que le problème qu'il résout soit un problème "universel" dégagé de présupposés subjectifs ». Brousseau précise que « nous appelons "dévolution" l'activité par laquelle le professeur cherche à atteindre ces deux résultats. ».

   Donc, partant du fait que dans notre population à profil entrant au lycée à dominance non scientifique « 38 % ont un profil d'entrée scientifique » et que 58 % n'ont pas de moyenne au baccalauréat en mathématiques avec un écart-type de 5,88, et que 34 % ont moins dr 5, c'est-à-dire que le tiers de la population ne reconnaît pas la terminologie qui peut permettre d'effectuer des algorithmes simples A4, tout cela démontre un écart significatif entre la pratique d'évaluation officielle et celle réelle. A savoir que parmi les rôles de l'évaluation on trouve l'évaluation diagnostique liée à l'acte d'enseignement, que l'évaluation officielle a prévu dans les documents officiels en la structurant par les analyses des acquis à chaque rentrée scolaire, ainsi que la programmation des contrôles continus, dont la pondération réelle dépasse celle prévue officiellement « 25 % pour le contrôles continu, 25 % pour l'examen régional qui comporte les matières littéraires (français, arabe, histoire géographie, éducation islamique), 0,50 % pour l'examen national ». Toutefois nous tenons à signaler un indice qui démontre le rôle important que joue la langue d'enseignement dans la phase A de R. Gras, en signalant que le taux de réussite pour les élèves orientés dans la filière du baccalauréat international option langue française était de 88,2 % en 2 016 année de rédaction de notre travail. Ceci peut s'expliquer par le fait d'unification du discours langagier au niveau de l'orale, l'écrit, ainsi que l'institutionnalisation du savoir, cet aspect d'unification de la langue d'enseignement permet l'instauration d'un contrat didactique visible pour les élèves, ce qui est opposé au contrat didactique dans une atmosphère multi-linguiste. De plus, dans le cas du contrat didactique visible au niveau langagier l'acte d'évaluation ne présente pas de coupure didactique dans son aspect de formulation, ce qui permet l'appropriation de la part des élèves des terminologies spéciales au discours mathématique, en plus de la cohérence entre le symbolisme dont la charge sémantique a un lien avec la langue véhiculée dans le cours mathématique, donnée que nous retrouvons pas dans l'architecture réelle du cours généralisé (dialecte, arabe, français et anglais).

   Quant à la structure des sujets d'examens de baccalauréat, nous constatons que depuis l'adoption des cadres de références d'une manière explicite de la part des décideurs pédagogiques (depuis l'an 2000) :

• La structure des sujets contient les niveaux A1, A4, B2, C1,C2,C4 de la taxonomie de R. Gras.

• Pour A2, les conditions d'administration d'un examen certificatif ne permettent pas de «bricoler, explorer », vu le temps limité réservé à la réalisation de l'épreuve par les élèves. Mais pour l'observation nous croyons que c'est une capacité nécessaire pour la réalisation de A3 à savoir la lecture des tableaux et des graphes, qui figure dans les épreuves des sciences de la vie et de la terre, et présente une difficulté au sens de G. Brousseau pour les élèves « une difficulté est un manque de moyens-savoir, pour résoudre une question ». Cela peut s'expliquer par le fait que la lecture des graphes n'est pas un objet d'enseignement au sens de R. Douady dans le cours des mathématiques, et devient outil de résolution dans les épreuves des sciences de la vie et de la terre. Autrement dit, nous constatons que l'influence des modèles des sujets d'examen adoptés en mathématiques agit négativement sur la pratique enseignante et l'oriente vers l'appropriation des algorithmes simples, et par conséquence devient un des éléments qui ne permettent pas la réalisation dans le curriculum réel des compétences transversales conçues par le curriculum officiel.

• Pour B1 qui mesure la capacité d'extension et d'induction, cela suppose son existence dans une situation d'évaluation du niveau C du cadre de référence, dont les caractéristiques sont d'être inhabituelles, et mobilise par synthèse des connaissances et résultats. Nous constatons comme nous l'avons signalé ci-dessous un vieillissement de situation d'évaluation qui ne produit plus de telle situation et par conséquence n'offre plus la possibilité de mesurer de telles capacités (induction et extension), sans oublier que le niveau B de R. Gras s'occupe de l'analyse des faits et de la transposition.

• Quant au niveau C de R. Gras qui mesure la compréhension des relations et structures selon des procédures exprimées en verbes opérationnels : reconnaître, construire, justifier, déduire, analyser, abstraire, appliquer, interpréter, comme nous l'avons indiqué ci-dessus pour C1, les sujets administrés aux évaluations du baccalauréat le place au niveau B du cadre de référence pour évoquer et appliquer de façon non explicite dans une question en incluant C2 et C4 dans son aspect d'application et d'interprétation, mais dans des situations habituelles des connaissances .

• Pour les niveaux D et E de la taxonomie de R. Gras qui s'attend à la mesure de la synthèse par le biais d'illustration, démonstration, la validation d'une production en situation évaluative pour le niveau D, ainsi que la critique et l'évaluation pour E par l'intermédiaire d'une modélisation qui met en relief les phases d'identification, différenciation, la classification, pour résumer et énoncer les hypothèses pour déduire et contrôler jusqu'à la phase de critique ou l'aboutissement à un résultat contradictoire.

   Pour les deux niveaux précédents D et E, nous constatons que la plupart des pays dont les performances sont au-dessous de la moyenne fixée par TIMS par exemple, ou qui se place dans des rangs alarmants par rapport à la norme internationale, leurs sujets d'évaluation certificative (le baccalauréat pour le cas du Maroc ou de la France) n'offrent pas ou rarement des situations qui atteignent ces niveaux (D et E), et par conséquence cela peut être un indice d'explication d'échecs des élèves issus des systèmes éducatifs qui ont une structure d'évaluation dominée par A, B et C de R. Gras.

Conclusions et pistes de recherches

   Nous tenons à préciser que notre étude du cas du système éducatif marocain, qui déclare par voix officielle le choix des compétences dans son curriculum, peut être généralisé pour tout autre système éducatif (nous pensons à la France, au Canada et aux autres pays qui adoptent l'approche par compétences au niveau officiel) qui adoptent l'approche par compétences, dans les différents cycles : primaire, collège, lycée et supérieur, et que l'analyse de la structure de l'évaluation est tout à fait justifiée du fait que l'approche par compétences cherche à développer la possibilité par les apprenants de mobiliser un ensemble intégré de ressources¹ pour résoudre une situation-problème. Par contre, l'approche par contenus considère l'enseignement en termes de listes de matières et de contenus-matières à enseigner, c'est-à-dire à transmettre. Quant à l'approche par objectifs, elle a comme porte d'entrée des comportements observables structurés, mais séparés les uns des autres, qui sont à développer chez les apprenants.

   Nous signalons que l'évolution des programmes officiels au Maroc comme dans d'autre pays francophones et anglophones a connu dans leurs développements depuis les années cinquante du siècle passé le passage de l'approche par contenus à l'approche par objectifs, pour aboutir à l'approche par compétences, sans pour autant que la conception de l'évaluation qui régit ce choix officiel dans ces systèmes ne reflète pas une structure cognitive basée sur la notion de compétences. Mais plutôt, comme nous l'avons démontré dans cet article, ils adoptent une optique des contenus, ce qui peut expliquer entre autres les carences constatées au niveau des évaluations internationales – TIMS – (pour le cas du Maroc et celui de la France par exemple). Nous précisons que les différentes approches entraînent des pratiques d'évaluation différentes (De Ketele & Dufays, 2003) :

• dans l'optique des contenus, évaluer consiste à prélever un échantillon de contenus représentatifs de l'univers de référence des contenus enseignés ;

• dans l'optique des objectifs, évaluer consiste à prendre un échantillon représentatif d'objectifs spécifiques et opérationnels et à produire un échantillon de questions qui traduisent au mieux cet échantillon d'objectifs ;

• dans l'optique des compétences, évaluer consiste à proposer une ou des situations complexes, appartenant à la famille des situations définie par la compétence, qui nécessitera (ont) de la part de l'élève-étudiant une production elle-même complexe pour résoudre la situation.

   Les épreuves conceptualisées à des fins d'évaluation selon chacune de ces approches seront inévitablement différentes. Néanmoins, les questions qui se posent par rapport à ces épreuves sont les questions classiques relatives à tout choix d'informations : sont-elles pertinentes, valides et fiables (De Ketele & Roegiers, 1993) ?

   Nous constatons que le cadre de référence du baccalauréat que nous avons examiné se situe dans l'optique d'approche des contenus, ce qui peut expliquer l'écart observé entre le curriculum officiel et le curriculum réel, et nous montre que la pratique évaluative réelle influence négativement la gestion ainsi que l'organisation de la pratique enseignante.

• La pertinence est le caractère plus ou moins approprié de l'épreuve, selon qu'elle s'inscrit dans la lignée des objectifs visés (De Ketele et al., 1989). C'est son degré de « compatibilité » avec les autres éléments du système auquel elle appartient (Raynal & Rieunier, 1997, 2003). Pour notre cas, il n'y a pas uniformité d'objectifs : le curriculum ainsi que les programmes officiels déclarent l'adoption des objectifs d'acquisitions de compétences, les cadres de références ont des objectifs de mesurer des habilités comme outil de mesure observable des compétences, tandis que les sujets administrés en acte d'évaluation n'atteignent pas tous les niveaux fixés par les cadres de références, et ils ne reflètent pas la notion de compétences par le biais des situations dites complexes. Par conséquence, la mesure de la pertinence doit avoir deux modalités : par rapport au curriculum officiel, et par rapport au cadre de références ; pour la modalité de curriculum, nous constatons que la pertinence n'est pas réalisée par les sujets administrés pendant l'évaluation certificative. Quant à sa valeur pour les cadres de références, nous pouvons affirmer qu'elle est réalisée avec des situations à caractères familiers par 80 %, vu qu'elle touche les niveaux A et B du cadre des références.

• La validité est le degré d'adéquation entre ce que l'on déclare faire (évaluer telle ou telle dimension) et ce que l'on fait réellement, entre ce que l'outil mesure et ce qu'il prétend mesurer (Laveault & Grégoire, 1997, 2002). Ce paramètre est pertinent pour mesurer l'écart entre le curriculum réel et le curriculum officiel, en particulier il permet d'élucider cet écart entre les cadres d'évaluation officielles et les situations d'évaluation réelles. Pour notre cas nous constatons, en nous basant sur le paramètre de validation, l'existence des écarts entre l'adoption d'approche par compétences de la part du curriculum officiel et la conceptualisation d'épreuve selon des contenus par les cadres de références. Quant aux sujets des épreuves de l'évaluation, nous pouvons conclure qu'il y a validité entre les objectifs déclarés et les contenus des sujets, cela malgré le constat du phénomène de vieillissement – Guy Brousseau – des situations d'évaluation qui instaure la mesure d'algorithmes devenus routiniers suite à la fixation d'un modèle précis avec des variations didactiques au niveau de nombres, de formes pour le cas algébrique et analytique comme cadres mathématiques, et au niveau de formulation pour le cas des probabilités et le cadre géométrique, cela malgré la déclaration selon laquelle les situations d'évaluation sont censées mesurer des habilités qui sont constituantes des compétences.

• La fiabilité est le degré de confiance que l'on peut accorder aux résultats observés : seront-ils les mêmes si on recueille l'information à un autre moment, avec un autre outil, par une autre personne, etc. ? Elle nous renseigne sur le degré de relation qui existe entre la note obtenue et la note vraie (Cardinet & Tourneur, 1985 ; Laveault & Grégoire, 1997, 2002). Il ne faut cependant pas perdre de vue que la note vraie est une abstraction, un point de convergence souhaité indépendant des évaluateurs et des circonstances ; ce paramètre est indice pour comprendre les scores bas des élèves des systèmes éducatifs en carence dans les évaluations internationales du genre TIMS ou PISA, étant donné que les outils de mesure internes adoptent une conceptualisation par contenus comme outil de mesure d'acquisition des connaissances-compétences. Par contre celle de TIMS particulièrement adopte une mesure selon l'approche par compétences, ce qui veut dire que les élèves subissent deux mesures issues de deux contrats didactiques différents, et par conséquences les scores ne seront pas les mêmes. De plus, si nous le constatons comme pour le cas de notre échantillon, ses individus manquent de seuil minimal de compétences à acquérir pour passer d'un cycle à l'autre ; ajouté à cela, leurs profils inadéquats à suivre des études scientifiques « 38 % ont un profil d'entrée scientifique ».

   Ces dimensions « La pertinence, la validité, la fiabilité » théoriquement indépendantes les unes des autres, forment ensemble des conditions nécessaires pour disposer d'une épreuve d'évaluation digne de ce nom. Mais, prises isolément, elles ne sont jamais suffisantes : un outil fiable peut très bien n'être ni valide, ni pertinent, ou un outil pertinent ni valide ni fiable, etc.

   Comme synthèse, on peut formuler que les épreuves-sujets élaborés des cadres de références – pour les mathématiques par exemple – proposent un ensemble d'items selon une structure très élaborée issue principalement d'une approche par les contenus et/ou les objectifs. Elles sont fiables et valides, mais ne sont pas pertinentes par rapport à l'approche par compétences et donc aux finalités des systèmes éducatifs conçus dans cet esprit. Si elles permettent bien d'évaluer les ressources jugées nécessaires (savoir-reproduire et savoir-faire), elles ne permettent pas (ou peu) d'évaluer la faculté de mobiliser celles qui sont pertinentes pour résoudre des problèmes ou effectuer des tâches complexes.

   Mais, par contre, nous tenons à signaler que nous sommes conscients des limites des épreuves selon l'approche par compétences, chose qui peut justifier l'adoption d'autres cadres pour l'évaluation comme celui de R. Gras, ou les cadres de références de TIMS.

   Les épreuves élaborées selon l'approche par compétences risquent cependant de présenter des difficultés de validité et de fiabilité étant donné la taille de l'échantillon issu de l'univers de référence. Par essence, ces épreuves vont consister à présenter à l'élève une, voire deux, situation(s) complexe(s), demandant de la part de l'élève une production elle-même complexe, nécessitant un certain temps de résolution. Les tâches demandées aux élèves varieront selon les situations.

• parfois la production sera constituée d'une tâche unique complexe, par exemple produire un texte répondant à une situation de communication,

• parfois la production pourra être décomposée en plusieurs tâches, comprenant elles-mêmes diverses étapes, sans qu'il soit nécessairement possible d'identifier le nombre exact d'étapes, comme c'est le cas par exemple dans la résolution de situations-problèmes mathématiques complexes où plusieurs voies de résolution sont possibles.

   Mais, en tous les cas, il ne sera pas possible de constituer un nombre d'« items », parce que ceux-ci reviendraient à décomposer la tâche complexe en sous-unités, ce qui ne permettrait plus d'évaluer la compétence qui consiste bien à gérer la complexité. Il n'est donc pas question, dans des épreuves d'évaluation construites selon l'approche par les compétences, de valider les outils comme on le fait avec des épreuves classiques (fondées sur les contenus et/ou les objectifs) en prenant comme unité d'analyse les « items » constituant l'échantillon issu de l'univers de référence. Dans une épreuve selon les compétences, ces « items » n'existent pas : il n'y a qu'une production complexe, ne constituant certainement pas un échantillon statistiquement représentatif de toutes les productions complexes possibles relativement à la compétence.

   Les techniques de validation des épreuves d'évaluation selon l'approche par compétences sont donc à inventer, avec d'autres postulats que ceux de la « théorie classique des scores ».

   Dans cette étape d'analyse nous proposons d'améliorer la taxonomie de R. Gras sous l'angle des questions suivantes : est-ce que les activités de R. Gras sont exhaustives ? linéaires ? ou dépendantes, cela dans le but de « dénicher » quelques pistes d'ingénierie d'évaluation à caractère dynamique qui permettra d'élaborer des situations d'évaluation qui ne souffrent pas de vieillissement au sens de Guy Brousseau.

   Nous pouvons postuler que la remédiation de l'écart constaté entre le curriculum imaginé-officiel et celui désiré dans les programmes et les manuels scolaires, ainsi que les cadres de référence d'évaluation, et le curriculum réel, peut se faire par l'adoption d'un cadre didactique tenant compte des aspects d'un concept qui se véhicule dans l'acte d'enseignement et la notion de sens qui mène à l'acquisition du sens du concept en le manipulant en tant qu'objet-outil au sens de R.Douady. Pour l'élaboration d'une taxonomie cognitive qui tient compte du processus d'acquisition d'une compétence dans les différents registres-cadres mathématiques, et qui permettra de mesurer les aspects de compétence (méthodologiques, communicatifs, technologiques, culturels), cette voix influencera par le biais d'évaluation la structuration des programmes scolaires-universitaires, par le fait de réalisation d'un saut informationnel au sens de Guy Brousseau d'une structuration dont le support didactique est « tableau noir-papier » à une structuration qui tient compte et encourage l'utilisation des TICS.

   Nous pouvons dire en conclusion que la différence entre des structures d'évaluation interne des systèmes éducatifs (contrôle contenus, examen régional, examen national pour le cas du Maroc et la structure réelle de l'orientation) et le choix d'approche par contenus, et la structure des évaluations internationales – TIMS et PISA en particulier – dont la structure d'évaluation a une tendance de structuration par la voie d'approche par compétences est parmi les explications des scores faibles enregistrés par les élèves issus de ces systèmes éducatifs. De plus les programmes nationaux des systèmes éducatifs qui participent à ces évaluations ne couvrent qu'une faible proportion du curriculum international – 30 % pour le cas du Maroc.

Said Haouassia,
shaouassia@yahoo.fr
El Mostapha El Khouzai

Laboratoire de l'ingénierie didactique et dynamique des systèmes (LIDDS), Établissement Faculté des Sciences et Techniques. Université Hassan 1^er, Settat, Maroc.

Cet article est sous licence Creative Commons (selon la juridiction française = Paternité - Pas de Modification). http://creativecommons.org/licenses/by-nd/2.0/fr/

Références

1. Guy Brousseau (1998). Théorie de situations didactiques, pensée sauvage, Grenoble, France.

2. M. Develay. Acte du colloque organisé à l'université de lyon2, 29 sept/2oct 1994. Le transfert des connaissances en formation initiale et en formation continue.

3. Correspondance avec Guy Brousseau, novembre 2011.

4. S. Haouassia. EpiNet n° 192 février 2017. Essai d'analyses didactique-statistique de la structure de l'évaluation-orientation. Cas du cycle du collège au Maroc.
   http://epi..asso.fr/revue/articles/a1702d.htm

5. Cadre de référence des examens du brevet, baccalauréat, Maroc, 2015.

6. Régine Douady. Jeux de cadres et dialectiques outil-objet dans l'enseignement des Mathématiques. Une réalisation dans tout le cursus primaire.. Histoire et perspectives sur les mathématiques. Université Paris VII, 1984.

7. R. Gras. EVAPM 2/03 / AB – DOC TAXO. Taxonomie d'objectifs congnitifs.16 septembre 2002.

8. Orientation officiel du ministère de l'éducation national. Maroc, 2008.

9. S. Haouassia. Rôle et utilisation de l'analogie dans la pratique enseignante, faculté des sciences de l'éducation, Rabat, Maroc, 1999.

10. Highlights From TIMSS and TIMSS Advanced 2015, Mathematics and Science Achievement of U.S. Students in Grades 4 and 8 and in Advanced Courses at the End of High School in an International Context, november 2016. U.S. department of education.

11. De Ketele, J.-M. (1993a). L'évaluation conjuguée en paradigmes, Revue Française de Pédagogie, 103, 59-80.

12. De Ketele, J.-M. (1993b). Objectifs terminaux d'intégration et transfert des connaissances, in Hivon, R. (éd.) L'évaluation des apprentissages. Réflexions, nouvelles tendances et formation, Sherbrooke (Canada), CRP, chap 1, 15-26.

13. De Ketele, J.-M. & Roegiers, X. (1991, 2e éd. 1993). Méthodologie du recueil d'informations, Bruxelles : De Boeck Université.

14. Raynal, F. & Rieunier, A. (1997, 4e éd. 2003). Pédagogie : dictionnaire des concepts clés, Paris : ESF éditeur.

15. Laveault, D. & Grégoire, J. (1997, 2e éd. 2002). Introduction aux théories des tests en psychologie et en sciences de l'éducation, Bruxelles : De Boeck Université.

16. Cardinet, J. & Tourneur, Y. (1985). Assurer la mesure, Berne – Francfort-s.Main – New York : Peter Lang.

17. Laveault, D. & Grégoire, J. (1997, 2e éd. 2002). Introduction aux théories des tests en psychologie et en sciences de l'éducation, Bruxelles : De Boeck Université.