Les tortues de Sofus
Alain Busser et Florian Tobé
Depuis la version 1.5, Le logiciel Sofus (langage de programmation Sophus dans un éditeur Blockly) permet le graphisme tortue, et même un mode multitortues. Dans cet article, on va décrire la genèse de cette fonctionnalité et la programmation objet qui a permis cette aventure. Pour mémoire, Sofus est un langage de programmation destiné au collège, dont l'interface Blockly permet une programmation graphique comme avec Scratch. Le mode tortue permet une transposition dans le champ graphique d'instructions typiquement sofusiennes comme augmenter x de 20 dont le pendant géométrique peut être avancer de 20.
1. L'objet Tortue
1.1. Propriétés
C'est lors d'un séjour à La Réunion, que Monsieur Sofus, naturaliste, a découvert une nouvelle espèce de tortue : La chelonia sofusia, ou « tortue de Sofus ». Cette tortue est munie d'un stylo svg, dont Monsieur Sofus s'est servi pour en dresser le portrait :

Grand consommateur de coffea arabica, Monsieur Sofus utilise le langage CoffeeScript pour décrire les espèces animales qu'il observe en milieu exotique. C'est donc dans ce langage sténographique qu'il a décrit les particularités de l'espèce chelonia sofusia ci-dessous. Dans ce langage, les fiches de Monsieur Sofus décrivant la tortue ressemblent à ceci :
class Tortue
constructor :
penup :
pendown :
show :
hide :
couleur :
tg :
td :
teleport :
av :
re :
distance :
azimuth :
Il a dénoté six particularités des tortues de Sofus :
- L'abscisse x, qui varie à chaque mouvement de la tortue en avant (av) ou en arrière (re ; voir ci-après). Au départ, elle est égale à l'abscisse du lieu de naissance de la tortue.
- L'ordonnée y, elle aussi initialisée à celle du lieu de naissance, et elle aussi laissée invariante par les rotations tg vers la gauche et td vers la droite.
- L'angle entre la tête de la tortue et l'Est magnétique, représenté par l'axe des abscisses (et à la naissance, la tortue est tournée dans cette direction).
Les tortues de Sofus, comme certains céphalopodes (la seiche par exemple), secrètent une encre qu'elles peuvent déposer sur le sable en laissant une trace, par une sorte d'aiguillon appelé stylo. La quatrième propriété d'une tortue de Sofus est la couleur de cette encre, qui, à la naissance, est le bleu noté #000066 en html. La magie des tortues de Sofus est qu'elles peuvent sur commande, changer la couleur de l'encre secrétée.
L'avant-dernière propriété des tortues de Sofus est la possibilité de lever le « stylo » afin de ne pas laisser de trace de leur passage. C'est une variable booléenne disant si le stylo est en état de marche.
Enfin, les tortues de Sofus, à l'instar des caméléons, peuvent changer d'aspect, en changeant de svg. Lorsqu'une tortue mue, elle change de costume qui est un groupe svg. La dernière des propriétés des tortues de Sofus est le numéro du costume, qui sert à référencer les costumes dans un tableau.
Ainsi, parmi les méthodes d'une tortue (voir ci-dessous), celle qui gère la naissance de la tortue a pour effet essentiel, outre la naissance elle-même, d'initialiser ces propriétés :
constructor : (@id) ->
@x = 320
@y = 240
@t = 0
@c = '#000066'
@stylo = true
@costumeId = 0
Les blocs de Blockly correspondant respectivement aux 4 premières propriétés de la tortue (x, y, t et c) sont les suivants :

Avec cette syntaxe, pour faire naître la tortue numéro 15 et la nommer toto, on écrit simplement toto = new Tortue 15 ce après quoi, on peut connaître l'abscisse de toto en écrivant toto.x. Le caractère arobase (@) veut dire « mon » et donc @x est « mon x à moi tout seul » pour la tortue dont on parle. La tortue présente au démarrage du logiciel Sofus a pour numéro 1, mais il est facile de faire naître une tortue de numéro entier quelconque, ce qui veut dire qu'il y a autant de tortues possibles, que d'entiers, ce qui sur un navigateur internet typique, est de l'ordre de 253=9007199254740992, ça fait tout de même beaucoup de tortues !
1.2. Méthodes
Les propriétés vues ci-dessus sont propres à chaque tortue : L'abscisse de Toto n'est pas forcément la même que celle de Tutu. Mais les méthodes sont ce qui fait des tortues de Sofus, que ce sont des tortues de Sofus : Elles font en quelque sorte partie de leur patrimoine génétique. De plus, elles font partie du savoir-faire des tortues de Sofus (ce sont des algorithmes). La liste en a été vue ci-dessus (fiche de Monsieur Sofus). Voici maintenant leur description et leur code génétique, en CoffeeScript :
Naissance : La méthode constructor a été vue ci-dessus.
C'est la seule qui ne s'appelle pas par toto.méthode() mais par new Tortue comme on l'a vu.
Visibilité : Voilà un exemple de « messages passés entre objets » : Pour cacher la tortue toto, il suffit de lui demander de se cacher, en lui envoyant le message toto.hide() ce qui va lui faire appliquer sa méthode hide (il va se rendre invisible). Mais comment va-t-il se rendre invisible, toto ? La question n'a d'importance que pour les programmeurs, pas pour les utilisateurs. Ceci dit, la méthode d'invisibilité est simple pour toto : Il modifie le Css de son propre svg, pour lui donner l'attribut « hidden ». Ce faisant, il appelle une méthode de jQuery qui s'appelle aussi hide() ; cette concision est la conséquence du fait que Sofus est une webApp :
show : -> $('#' + @id).show()
hide : -> $('#' + @id).hide()
Les blocs de Blockly permettant d'utiliser les méthodes hide et show sont ceux-ci :

1.3. Stylo : Méthodes penup(), pendown() et couleur()
Monsieur Sofus a longuement étudié la manière dont fonctionne le stylo (appendice permettant à la tortue de Sofus, de projeter de l'encre par terre). Voici l'extrait de son carnet de notes consacré à ce sujet qui a fait couler beaucoup d'encre (par la tortue) :
pendown : -> @stylo = true
penup : -> @stylo = false
couleur : (coul) -> @c = coul
Pour appliquer la méthode penup, la tortue met son stylo (@stylo) à false. Pour baisser le stylo, elle met la même variable à true. Et pour choisir la couleur coul, elle met sa variable c à la couleur coul. Les blocs de Blockly permettant d'utiliser ces méthodes sont les suivants :

1.4. Les rotations : tg et td pour tourner à gauche ou à droite
Pour tourner la tortue vers la gauche, il suffit de soustraire à son angle @t l'angle de rotation ; pour tourner la tortue vers la droite, il suffit d'additionner l'angle. Et pour orienter la tortue selon un angle donné, il suffit d'imposer que son angle @t soit la direction voulue. Voici comment Monsieur Sophus a rédigé les phénotypes correspondants :
tg : (a) ->
@t -= a / 180 * Math.PI
td : (a) ->
@t += a / 180 * Math.PI
Et voici les blocs de Blockly permettant de faire tourner la tête à Toto :

1.5. Déplacement
Pour avancer de d pixels, la tortue doit :
Mémoriser ses coordonnées actuelles dans deux variables oldx et oldy ;
Ajouter à son abscisse, le produit de d par le cosinus de l'angle @t, et à son ordonnée, le produit de d par le sinus de @t ;
Si le stylo est levé, c'est tout, il y avait juste les coordonnées à modifier. Mais sinon, il y a un segment à tracer, dont l'origine a pour coordonnées (oldx,oldy), dont l'extrémité a pour coordonnées (@x,@y) et dont la couleur est @c (couleur de l'encre secrétée par la tortue de Sofus)
Rédigé en CoffeeScript, ce code s'écrit :
av : (d) ->
oldx = @x
oldy = @y
@x += d * Math.cos(@t)
@y += d * Math.sin(@t)
dessineSegment(oldx, oldy, @x, @y, @c) if @stylo
Alors pour faire avancer tutu de 80 pixels on lui envoie le message tutu.av 80. Pour faire reculer la tortue, la méthode est similaire sauf qu'au lieu d'additionner, on soustrait. Les blocs de Blockly permettant à la tortue de bouger sont les suivants :
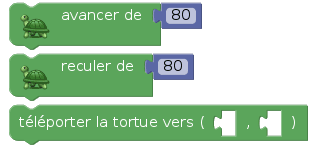
1.6. Téléportation
On voit ci-dessus un bloc permettant de téléporter la tortue vers deux coordonnées absolues. En effet, des tortues capables de se rendre invisibles, ont même le pouvoir de téléportation. La méthode est une fonction des deux coordonnées (x,y) de la destination, et consiste simplement à remplacer les coordonnées actuelles de la tortue par x et y :
teleport : (x, y) ->
[@x, @y] = [x, y]
2. De la tortue aux tortues
M. Sofus n'était pas aux bout de ses surprises. Non content d'avoir trouvé cette superbe chelonia sofusia, il s'aperçut au détour d'une plage dans le fond de Terre Sainte, non loin de la « Pointe à Gérard », que la chelonia sofusia appartenait en fait à une colonie. Il y avait des tortues « en veux tu ? En voilà ! ». M. Sofus était donc confronté à un nouveau problème : comment tenir un registre de l'ensemble de ces tortues ? Il décida de les numéroter afin de les identifier de manière unique. Ainsi, il n'aurait plus qu'à associer à chaque identifiant une fiche tortue. Prenant sa plume, il écrivit dans un CoffeeScript parfait son premier registre qu'il appela naturellement totos (au pluriel !). Évidemment, ce registre était complètement vide !
totos = {}
Ne restait plus qu'à le remplir en ajoutant une à une les tortues :
totos[1] = new Tortue 1
totos[2] = new Tortue 2
...
totos[1000] = new Tortue 1000
Ou encore mieux :
totos[n] = new Tortue n for n in [1..1000]
Du coup, lorsqu'il désirait lire, spécifier ou modifier un des attributs de la tortue, il n'avait plus qu'à faire appel à son registre pour la retrouver, en précisant l'attribut visé. Ainsi, pour changer la couleur de l'encre secrétée par la tortue 1 en bleu, il écrivit :
totos[1].c = '#000066'
Orienter les tortues devint un jeu d'enfant. En effet, un pivot à 35° devait s'écrire ainsi :
totos[1].orient 35
Pour manipuler l'ensemble de ses tortues, il dût se résoudre à modifier quelque peu ses conventions. toto ne désignerait plus une tortue mais un identifiant pour le registre totos. La toto 1 serait dorénavant désignée par totos[toto] à condition que toto vaille 1 :
totos = {}
toto = 1
totos[toto] = new Tortue toto
alert "id de la toto 1 : #{totos[toto].id}"
# Affiche une alerte : "id de la toto 1 : 1"
Lors de mouvement d'envergure impliquant plusieurs tortues, deux par exemple, cette variable toto servirait de curseur à tortue. Tel l'archimède des temps modernes, il s'écria « Euchelonia » lorsqu'il découvrit qu'aux origines naissaient les tortues !
totos[n] = new Tortue n for n in [1..2]
toto = 1
x1 = totos[toto].x
y1 = totos[toto].y
toto = 2
x2 = totos[toto].x
y2 = totos[toto].y
alert "Euchelonia !" if x1 is x2 is y1 is y2 is 0
# Affiche une alerte : "Euchelonia !"
Découvrant dans sa stupeur que toto 1 et toto 2 étaient un peu trop proches, il déblocka et le block « Avec la tortue » était né !
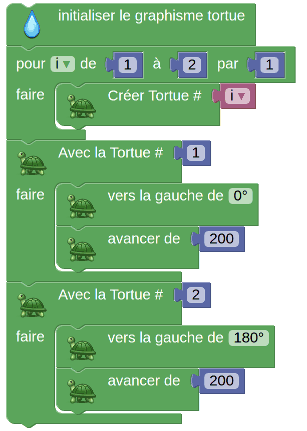

Content de lui, il s'assoupit quelque peu du sommeil du juste, en rêvant à toutes les sauces auxquelles il cuisinerait ce petit registre (pas l'instance pour les tortues, mais son prototype !).
Pendant son sommeil, des professeurs de mathématiques ont cherché à quoi ces tortues pourraient leur servir, voici quelques exemples de ce qu'ils ont trouvé.
3. Applications
3.1. Avec une seule tortue
3.1.1. Tout d'abord, le classique tracé d'un pointillé :
Cette activité aborde à la fois la notion de stylo et la notion de boucle : Pour avancer de 200 pixels, la tortue va répéter 10 fois l'action d'avancer de 20 pixels. Cette complication permet d'insérer des mouvements de stylo entre les pas :
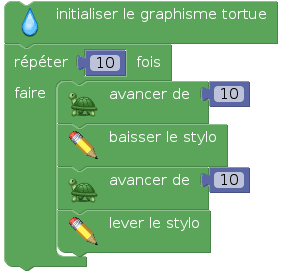
En apparence, la tortue dessine sur du sable, en réalité le dessin se fait sur un calque svg, transparent, posé sur le sable. On peut récupérer ce calque en cliquant sur le bouton « svg », et le voici :
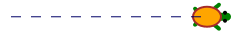
3.1.2. Un peu de récursivité avec le flocon de Von Koch
On crée ici une fonction (ou procédure : Elle ne renvoie rien) appelée koch, qui trace une courbe de Von Koch au rang n, en demandant à la tortue de faire les choses suivantes :
Tracer une courbe de Von Koch au rang n-1 ;
Tourner de 60° vers la gauche ;
Tracer une courbe de Von Koch au rang n-1 ;
Tourner de 120° vers la droite ;
Tracer une courbe de Von Koch au rang n-1 ;
Tourner de 60° vers la gauche ;
Pour éviter d'avoir besoin d'un microscope, on convient que la courbe de Von Koch au rang 0 est un segment de longueur 1,4 pixel. Le script est donc le suivant :
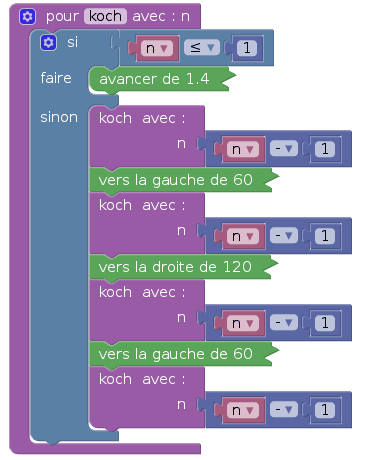
Avec ça, pour tracer le flocon de neige de Von Koch, on trace 3 courbes de Von Koch et entre deux tracés, la tortue tourne de 120° vers la droite :
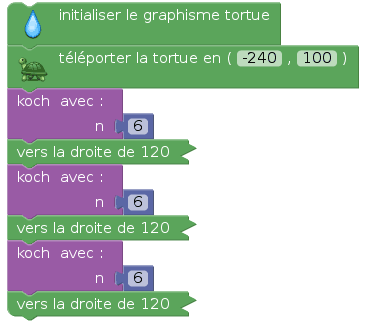
La tortue trace bien la célèbre star de l'infographie (qui est plus que centenaire ; la star, pas l'infographie) :

3.1.3. Spirales
Le tracé d'un carré est un grand classique de la tortue : Répéter 4 fois l'action d'avancer d'une certaine longueur (le côté du carré) et de tourner de 90°. Mais pour peu que la longueur pas (nombre de pas...) dont la tortue avance, augmente à chaque rotation, on obtient une spirale :
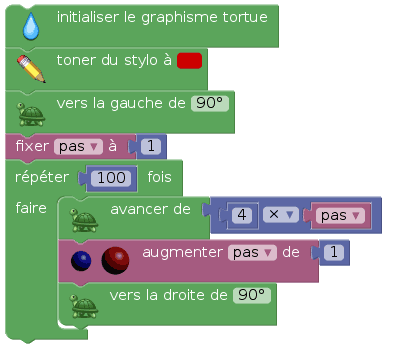
On obtient cette spirale rouge :

On aurait pu avancer de pas pas puis augmenter pas de 4 ; on a préféré avancer de 4×pas pas et augmenter pas de 1. Cela paraît plus compliqué mais donne un sens à la variable pas : C'est le nombre de « pas élémentaires » que parcourt la tortue pour chaque côté de la spirale. On peut encore compliquer les choses en demandant à la tortue, au lieu d'avancer de 4×pas, de répéter pas fois l'action d'avancer de 4 pixels. Cette complication permet de passer facilement à la spirale d'Ulam.
La tortue se transforme en petit Poucet et dépose des cailloux (stylo levé) ; en plus, elle ne dépose pas de cailloux systématiquement, mais seulement si le nombre total de pas élémentaires depuis le début du trajet (un compteur N) est premier :
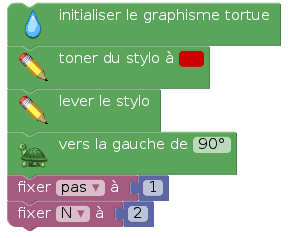
Après l'initialisation de la figure, on effectue cette boucle :
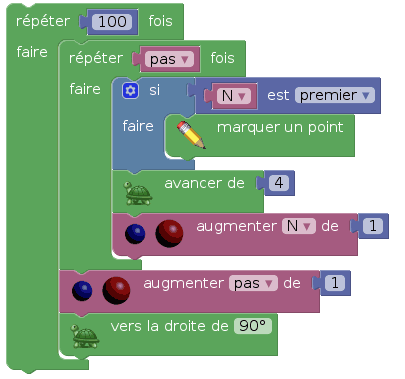
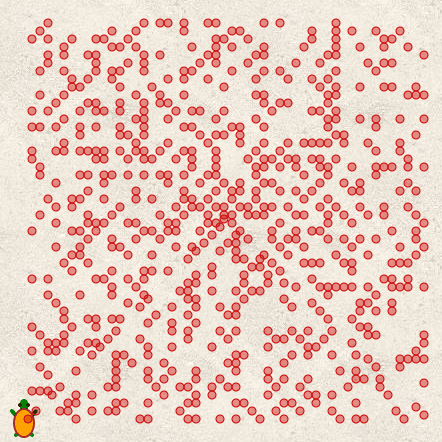
Voici alors la spirale d'Ulam :
3.2. Avec plusieurs tortues
3.2.1. Une petite course poursuite ?
Monsieur Sofus a été contacté par l'entreprise Monsantoto, qui cherche à modifier génétiquement des tortues pour qu'elles soient prédatrices. Ici c'est la tortue numéro 2 qui poursuit la tortue numéro 1, mais elle n'arrive pas à la rattraper parce qu'elle n'avance que de 0,7 pixel à chaque pas :
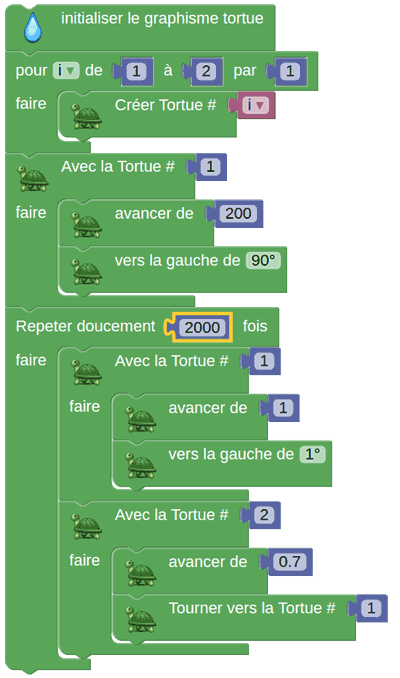

Monsieur Sofus a refusé l'offre qui lui fut faite par Monsantoto : Il a répondu « Non, sans Toto ! » à Monsantoto.
3.2.2. Diagramme en bâtons
Voici une application des tortues à la statistique : Le dessin d'un diagramme en bâtons. On lance 1 000 fois de suite deux dés, et on représente graphiquement le diagramme en bâtons des effectifs de la somme de ces dés. Le script proposé est une forme de calcul parallèle en ce que chaque tortue mémorise, sous la forme de son ordonnée, l'effectif qui lui correspond. Aucune tortue ne sait où sont les autres tortues, ce qui est typique du calcul parallèle.
Avant de lancer les dés, on crée des tortues de numéros 2 à 12 parce que la somme des dés ira de 2 (1+1) à 12 (6+6) :
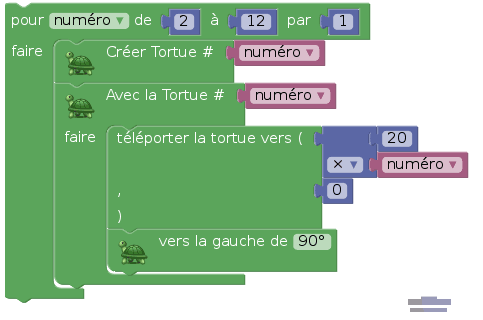
Chaque tortue est téléportée vers le bas du bâton qu'elle va dessiner, puis tournée vers le haut pour que le bâton soit dans le bon sens. Une fois effectuée cette initialisation de l'algorithme, on lance 1 000 fois les dés, on les additionne et on demande à la tortue correspondant à la somme de mettre à jour le diagramme en bâtons. Par exemple, si la somme des dés vaut 7, on demande à la tortue numéro 7 d'avancer d'un pixel. On a ici une situation typique de la programmation objet : Seule la tortue numéro 7 doit avancer, et on obtient ce comportement en lui envoyant un message. On remarque que le message est englobé dans un bloc en forme de « C » (ici le message ne comprend que l'instruction « avancer de 1 ») :
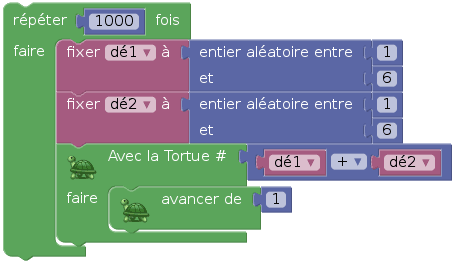
Ce script suffit à dessiner le diagramme en bâtons :
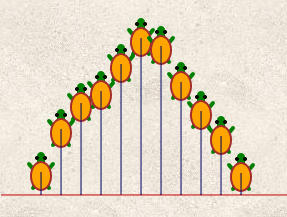
On peut améliorer ce diagramme en demandant aux tortues de se cacher, et de « tamponner » leur ordonnée finale. On peut également constituer un tableau avec ses ordonnées ou les afficher dans la sortie numérique de Sofus, laquelle peut être copiée-collée dans un fichier texte avant de l'enregistrer avec l'extension « csv » ce qui permet alors de l'ouvrir dans un tableur.
4. Et ensuite ?
L'idée de faire manipuler des robots virtuels par les enfants, pour les réconcilier avec l'abstraction mathématique, est un peu paradoxale. Cette idée remonte aux années 1970 avec Minsky et Papert. Ils ont alors transposé à l'écran de l'ordinateur des robots construits à la fin des années 1940 par Grey Walter : Les tortues de Bristol. Ce genre d'activités avec les tortues virtuelles laisse sur le côté les élèves qui ont besoin de toucher pour apprendre, les aveugles et les mal voyants. Sans parler du plaisir de manipuler... Or Blockly permet de commander des machines comme les Arduino avec des interfaces comme BlocklyDuino. On peut penser aussi au robot Picaxe ou à des robots faits avec le Raspberry Pi. Il ne semble pas difficile de refaire la programmation des tortues avec ces machines, et d'avoir la possibilité de faire des dessins sur papier A3 dans des séances où le robot fait des taches partout avec l'encre qui coule, où des élèves tentent de perturber le robot en lui bloquant le passage, etc. Dans ce cas, la téléportation du robot sera effectuée manuellement par l'élève, ce qui permettra d'aborder la notion de coordonnées. Idéalement, ce genre de séance serait bien entendu abordé en EPI (maths-arts plastiques avec des robots tout faits, ou maths-techno si ce sont les élèves qui modifient Blockly pour piloter les robots).
Alain Busser
Florian Tobé
Cet article est sous licence Creative Commons (selon la juridiction française = Paternité - Pas de Modification).
http://creativecommons.org/licenses/by-nd/2.0/fr/
|