Sophus, un langage de programmation pour le collège

Alain Busser
 

   Lors de travaux dirigés d'algorithmique en terminale, et de la correction de copies de bac, il a été constaté que, souvent, une simple affectation comme x := x+1 est déjà trop complexe pour beaucoup d'élèves. Plusieurs écrivent des choses comme « effectuer x+1 » sans trop savoir quoi faire du résultat de l'addition, une fois celle-ci effectuée. Une difficulté similaire apparaît lorsqu'on doit répéter une certaine action dans une boucle, puisque pour cela il faut créer une variable « indice » destinée à être incrémentée à chaque passage dans la boucle, et que cette incrémentation se fait par indice := indice+1. Le besoin d'un langage de programmation sans affectation ni indices de boucles visibles, s'est alors fait sentir. C'est ainsi qu'est né Sophus.

   Le langage tire son nom de la théorie des groupes de Lie, qui consiste justement à modifier des nombres (ou des tuples ou des matrices) par transformations successives. En effet, le créateur de cette théorie s'appelait Sophus Lie.

   Il y a un interpréteur Sophus en ligne [1] qui permet de tester le langage. Pour l'utiliser hors ligne, on peut le télécharger sur github. On a alors un dossier bloquement qui permet également de programmer en Sophus au sein de Blockly. C'est d'ailleurs de ce dernier que proviennent les copies d'écran ci-dessous.

Trois idées

   Sophus est un langage de programmation en langue française (comme LSE et Algobox) mais axé sur la modification de variables sans affectations. Ce qui rend ce langage nouveau est, paradoxalement, la réunion de trois idées anciennes et quelque peu disparues avec le temps :

1. Les boucles « until » ou « jusqu'à » en français, qui existaient dès la fin des années 1960 en Pascal (Niklaus Wirth) à côté des boucles « while » mais ont fini par être éclipsées par celles-ci parce que la redondance a paru inutile. Cependant, chaque négation occupant un élément de mémoire de travail chez les élèves, ceux-ci comprennent mieux des phrases sans négation. Or la boucle « jusqu'à » est équivalente à une boucle « tant que » et une négation. Par exemple, voici la version classique de l'algorithme d'Euclide avec « while » :

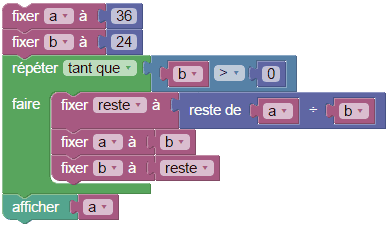
   Alors que la version « jusqu'à » est

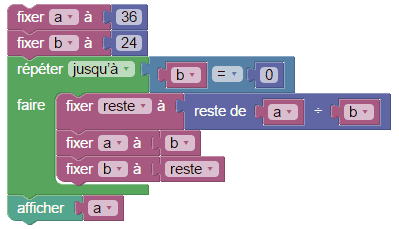
les boucles sans utilisation explicite de l'indice. Celles-ci ont été inventées dans les années 1960 par Seymour Papert au MIT, qui les a implémentées en Logo : Pour dire à la tortue qu'elle doit faire 5 fois un dessin, on n'a pas vraiment besoin de savoir compter, et la programmation s'en trouve souvent simplifiée. Ces boucles ont été reprises par Alan Kay avec Smalltalk et ont donc naturellement survécu dans Scratch et Blockly. Pour afficher quatre puissances successives de 2 (2¹, 2², 2³ et 2⁴⁾ en Sophus, on peut faire ceci :

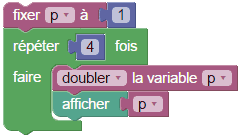
2. L'idée la plus caractéristique de Sophus est la modification de variables sans affectation explicite, qui remonte au langage Cobol en 1959 (équipe dirigée par Grace Hopper). Par exemple pour calculer par la méthode des rectangles l'intégrale de la fonction logarithme entre 1 et 2, on peut tenter ce script où x et y sont des variables et dx une constante :

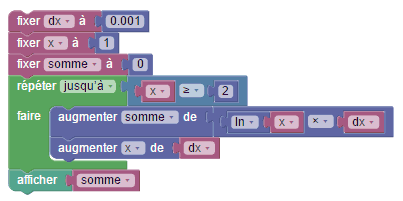
3. Voici un résumé de l'algorithme, où dx est une constante et x et somme sont des variables :

• x est initialisé à 1 parce qu'on calcule l'intégrale entre 1 et 2 ;
• somme est une variable de type « compteur », donc initialisée à 0 ;
• on boucle jusqu'à ce que x dépasse 2 (borne supérieure de l'intégrale) :
• On ajoute ln(x)dx à la variable somme ;
• On ajoute dx à x ;
Ainsi, à la fin, x est allé de 1 à 2 par pas de dx, et somme contient la somme des ln(x)dx qui est donc l'intégrale ∫¹2ln(x)dx.

Programmes de calcul au collège

   Un programme de calcul est une suite de modifications d'une (ou deux) variable numérique, et Sophus est donc particulièrement adapté au volet numérique de la programmation au collège.

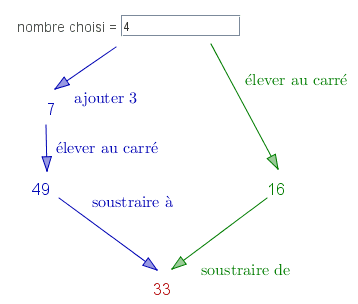
   Voici un extrait du sujet du brevet des collèges Polynésie 2015 :

1. Voici un programme de calcul :

Programme A

• Choisir un nombre.
• Ajouter 3.
• Calculer le carré du résultat obtenu.
• Soustraire le carré du nombre de départ.
1. Eugénie choisit 4 comme nombre de départ. Vérifier qu'elle obtient 33 comme résultat du programme.
2. Elle choisit ensuite –5 comme nombre de départ. Quel résultat obtient-elle ?

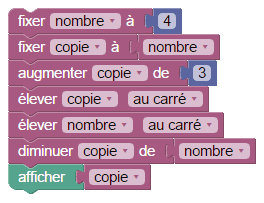
   Pour programmer ça en Sophus, on a besoin de mémoriser le nombre de départ, puisqu'on l'élève au carré après l'avoir modifié. C'est donc une copie que l'on va modifier avant de lui soustraire le carré du nombre de départ :

   Et voici la suite du sujet du brevet Polynésie 2015 :

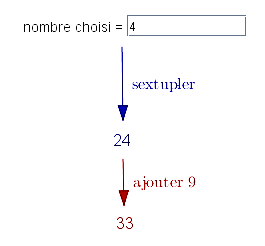
2. Voici un deuxième programme de calcul :

Programme B

• Choisir un nombre.
• Multiplier par 6.
• Ajouter 9 au résultat obtenu.

   Clément affirme : « Si on choisit n'importe quel nombre et qu'on lui applique les deux programmes, on obtient le même résultat. »
Prouver que Clément a raison.

   Celui-là est plus facile à programmer :

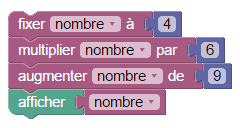
   Et on peut même faire encore plus simple :

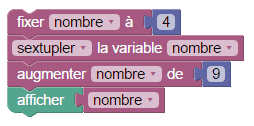
   En activité de programmation, ce genre d'exercice numérique aide à appréhender l'algèbre (on montre que (x+3)² – x² = 6x + 9 par développement et réduction) et les priorités opératoires. Mais aussi, par comparaison avec la tortue Logo, on peut découvrir les similitudes qu'il y a entre les programmes de construction (le programme B est la composée d'une homothétie de rapport 6 et d'une translation de vecteur de norme 9), et les programmes de calcul (là c'est Sophus que entre en scène). Sophus n'étant pas doté de graphisme, on gagnera à inscrire quelques séances Sophus dans une progression incluant également des activités graphiques, comme

• Le tracé de figures avec la tortue Blockly [2].
• Le parcours d'un labyrinthe [3].
• La logique des tests [4].
• L'algèbre sans peine [5].

Fractions

   Toujours au collège, on peut utiliser Sophus pour explorer le monde redoutable des fractions. Voici un énoncé plus difficile qu'il n'y paraît :

   Une forêt contient 2 500 arbres adultes. Un pyromane, en déclenchant un incendie, brûle les deux cinquièmes de la forêt. Combien d'arbres reste-t-il après l'incendie ?

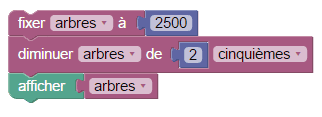
   Voici un programme en Sophus permettant de calculer ce nombre :

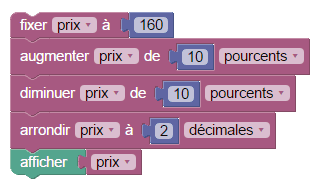
   Le menu déroulant qui, entre autres, comprend le dénominateur « cinquièmes », possède également une option « pourcents » ce qui permet de calculer avec les pourcentages, comme par exemple pour calculer le prix après une remise de 10 pourcents. Cela permet également de comprendre que les pourcentages ne sont qu'un cas particulier de fractions. On peut très rapidement écrire un programme Sophus permettant de voir l'effet d'augmentations et diminutions consécutives d'un pourcentage donné :

   Ici on constate que le nouveau prix n'est pas de 160 € donc qu'une augmentation de 10 % n'est pas exactement compensée par une diminution de 10 %.

   En résumé, Sophus est au calcul ce que Logo est au dessin : On opère par touches successives, et on explore ainsi un micromonde qui permet de construire le savoir numérique et algorithmique. L'intégration de Sophus à Blockly, initiée par Patrick Raffinat [6], permet de mettre en place des séquences pédagogiques mixtes (numériques + géométriques). Et la future intégration de Blockly dans DGPad [7] laisse prévoir que de telles activités mixtes puissent être faites entièrement sous DGPad...

Bonus : Calcul de π

   L'algorithme suivant de calcul de π est dü à François Viète, et converge plutôt vite :

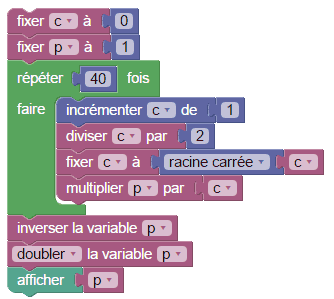
   La valeur de π calculée avec 40 boucles est précise à 10^-15 près. Voici quelques exemples :

Alain Busser,
IREM de La Réunion

Cet article est sous licence Creative Commons (selon la juridiction française = Paternité - Pas de Modification). http://creativecommons.org/licenses/by-nd/2.0/fr/

NOTES

[1] http://irem.univ-reunion.fr/spip.php?rubrique173

[2] https://blockly-games.appspot.com/turtle?lang=fr

[3] https://blockly-games.appspot.com/maze?lang=fr

[4] https://blockly-games.appspot.com/bird?lang=fr

[5] https://blockly-demo.appspot.com/static/demos/plane/index.html?lang=fr

[6] http://www.epi.asso.fr/revue/articles/a1510c.htm

[7] http://www.dgpad.net/index.php?lang=FR