Contribution des enseignants de mathématiques
au concours des enseignants innovants au Maroc

Brahim Nachit, Ahmed Lablidi, Namir Abdelwahed,
Mohamed Bahra et Mohammed Talbi
 

Résumé
L'enseignement mobilise beaucoup de ressources (manuel - site web - ressource en ligne...) pour parer autant que possible, aux difficultés d'enseignement et d'apprentissage et redonner du sens aux concepts. Le Ministère de l'Éducation nationale encourage l'intégration des TIC dans l'enseignement. Il organise chaque année un concours des enseignants innovants, les enseignants de mathématiques participent régulièrement à cette manifestation.

Dans cet article, nous avons évalué la participation des enseignements de mathématiques à ce concours, nous avons aussi montré que les enseignants de mathématiques sont les plus primés pendant les sept premières éditions du concours.

Mot clés : Innovatice, ressources numériques, sens, TIC, enseignants innovants.

Note de la rédaction EPI : Concernant l'initiative « enseignants innovants » de Microsoft en France voir entre-autres :
http://www.epi.asso.fr/revue/docu/d1303a.htm
http://www.framablog.org/index.php/post/2008/02/16/forum-enseignants-innovants-microsoft-partenaire
http://www.framablog.org/index.php/post/2008/02/19/forum-des-enseignants-innovants-suite-et-fin

Introduction

   Beaucoup de travaux en didactique des mathématiques ressortent les difficultés des élèves liées à l'apprentissage de plusieurs concepts. C'est le cas des fractions (Rosar et al., 2001) et de l'algèbre (Chevallard, 1989).

   Les connaissances et les compétences mathématiques de la plupart des élèves ne sont pas satisfaisantes, on peut se référer aux résultats TIMSS (Trends in Internationale Mathématics and Science Study) de l'ISC (International Study Center) et PISA (Programme International pour le Suivi des Acquis des élèves).

   L'enseignement des mathématiques dans la scolarité de base est selon la commission européenne, 2007) :

• Conçu comme un enseignement formel, centré sur l'apprentissage des techniques et de mémorisation des règles ;
• Le lien avec le monde réel est faible ;
• Les pratiques expérimentales et les activités de modélisation sont rares ;
• L'utilisation pertinente de la technologie reste relativement limitée.

   Certains enseignants perdent parfois le plaisir d'enseigner. Selon Belli et Pech (2006), cette perte de plaisir se traduit le plus souvent par le fait que :

• Les exercices proposés sont souvent des situations déconnectées de la réalité ;
• Les exercices sont typiques et se résolvent de la même façon ;
• La mémoire est énormément sollicitée ;
• Les enseignants s'investissent peu dans les activités des élèves.

   Les difficultés des élèves se regroupent autour des problématiques suivantes :

• Les bases minimales de l'enseignement primaire ne sont pas assurées ;
• La transition primaire-secondaire est difficile, on passe d'une mathématique basée sur le concret vers une mathématique plus abstraite, le passage au raisonnement abstrait pose problème ;
• Il existe des problèmes spécifiques aux mathématiques : L'activité mathématique est souvent perçue comme une activité loin du monde réel et purement formelle ;
• Le problème de "sens" : la plupart des élèves n'arrivent pas à comprendre le sens de plusieurs concepts enseignés.

   Ces difficultés conduiraient à « des échecs et à des abandons, à une dévalorisation de soi, à une impuissance à se prendre en main et à des tentatives infructueuses pour comprendre les vraies raisons de l'échec » (Lafortune 1997, p.4), la plupart des élèves abordent les mathématiques avec réticence, par obligation et sans plaisir (ibid., 1997, p.13).

   L'enseignement des mathématiques de qualité doit permettre aux élèves de comprendre que la mathématique est une science vivante, en relation avec le monde réel et qui contribue à la résolution de ses problèmes, loin des stéréotypes qui lui sont attachés dans la culture commune. Cet enseignement doit permettre de vivre l'expérience mathématique, et pour cela il doit s'appuyer sur les technologies de l'information et de communication (TIC).

   Selon (Hoyles et Lagrange, 2009), les technologies ont enrichi de façon indéniable les possibilités d'expérimentation, de visualisation et de simulation, elles ont permis de traiter des problèmes plus réalistes.

   Pierre Couillard (2004) estime que « en utilisant ces technologies, les enseignants et les enseignantes ont à leur disposition des outils puissants qui peuvent amener les élèves beaucoup plus loin dans leurs apprentissages que l'enseignement traditionnel. Les statistiques, la géométrie, la numération, les opérations de base et l'algèbre peuvent prendre un sens « réel » avec la bonne intégration des TICE dans la démarche d'apprentissage des élèves ».

   Les nouvelles technologies assurent l'accès en ligne aux ressources, la production collaborative et la multiplication de ressources aident à l'émergence de communautés d'enseignants et de chercheurs et à l'échange à distance entre élèves et enseignants. (Hoyles et Lagrange, 2009) montrent que des possibilités nouvelles s'ouvrent pour faciliter l'accès aux ressources et à la formation et favoriser la diffusion des idées et des innovations. L'enseignement des mathématiques a besoin de ressources de qualité pour les élèves et les enseignants et ceci pour affronter les difficultés d'enseignement-apprentissage.

   Gueudet et Trouche (2009) montrent des évolutions rapides portées par l'évolution technologique avec la multiplication des ressources accessibles en ligne, il y a là de nouvelles possibilités pour la conception des ressources.

   En effet, pour Gérard Kuntz « l'étude attentive, au cours des dernières années, de l'important mouvement de création de ressources mathématiques en ligne, conduit de nombreux observateurs à la conviction que le renouvellement de l'enseignement des mathématiques se prépare et se dessine sur Internet » (Kuntz, 2007, p. 104).

   Les enseignants marocains de mathématiques produisent des ressources numériques pour faciliter l'enseignement et l'apprentissage, ils participent régulièrement au concours des enseignants innovants organisé chaque année par le Ministère de l'Éducation nationale (MEN).

   Plusieurs produits multimédias étaient conçus par des enseignants innovants de différentes disciplines. Dans cet article, nous analysons les documents de références du concours et les listes des enseignants innovants primés des éditions (2005-2011) et nous nous intéressons plus particulièrement aux productions primées en mathématiques.

   Notre objectif est d'évaluer la participation des enseignants de mathématiques au concours des enseignants innovants au Maroc et leurs produits primés durant les sept premières éditions du concours.

Contexe du projet

   « Innovatice », le forum de l'Éducation innovante s'inscrit dans le cadre de la charte nationale de l'éducation et de formation (CNEF) qui vise dans le levier 10 à :

• Optimiser l'emploi des ressources éducatives technologiques et tirer meilleur parti des technologies modernes.

• Investir les TIC en tant que voies de l'avenir pour parer autant que possible aux difficultés d'enseignement ou de formation continue des enseignants.

   Le forum est le fruit de la coopération entre Microsoft Maroc et le MEN dans le cadre de l'initiative (partenaires in Learning). Il s'agit d'un concours national ouvert à tous les éducateurs du Royaume ayant présenté des projets pédagogiques innovants visant à faciliter l'apprentissage et l'enseignement des différentes disciplines (Mathématiques, physique- chimie, français...).

   Ce concours est organisé par une note ministérielle accompagnée d'un dossier qui comprend :

• Les textes organisationnels ;
• Le cahier de charge ;
• La pièce jointe qui comprend des informations sur l'enseignant innovant.

   Le concours national est caractérisé par l'offre de trois types de prix :

• Prix des meilleures productions multimédia présentées par les enseignants exerçant en classe de manière individuelle (MMI) ;
• Prix des meilleures productions multimédia présentées dans le cadre d'un travail en groupe (MMG) ;
• Prix des meilleurs scénarios pédagogiques utilisant les TIC (SPTIC).

Critères d'évaluation

   La sélection des acteurs pédagogiques à primer se fait en trois phases :

   La première phase : Cette phase d'évaluation des produits multimédia se fait par des commissions constituées des inspecteurs des matières objet du projet, cette évaluation se fait selon des critères tel que : le contenu du produit, l'utilisation pédagogique et l'innovation pédagogique.

   La première phase d'évaluation pour les scénarios pédagogiques se fait par des commissions constituées de deux inspecteurs de chaque matière sur la base des critères tels que : le choix du sujet, les compétences à développer et le problème à résoudre.

   La deuxième phase : Se fait par des jurys de professionnels qui évaluent les projets sélectionnés lors de première phase pour en déterminer les projets les plus innovants.

   La troisième phase : Aux mêmes jurys s'ajoutent d'autres experts de l'évaluation des ressources numériques, lors de cette étape, les acteurs pédagogiques, porteurs des projets présélectionnés passent un entretien axé principalement sur la présentation générale du projet, la maîtrise du sujet, l'importance du scénario pédagogique et la maîtrise de l'usage des TIC.

Objectifs du concours

Le forum de l'Éducation innovante a pour objectifs de :

• Valoriser les enseignants qui innovent par l'introduction des TIC dans leurs pratiques pédagogiques ;
• Contribuer à la diffusion et au partage des ressources entre les acteurs de l'Éducation ;
• Développer les compétences professionnelles des éducateurs dans l'intégration des TIC dans l'enseignement ;
• Créer une banque de ressources numériques compatibles avec les programmes nationaux ;
• Encourager l'intégration des TIC dans le processus enseignement-apprentissage ;
• Constituer un réseau des enseignants innovants pour diffuser et partager les expériences ;
• Créer un dynamisme et une compétitivité entre les acteurs pédagogiques des différents niveaux scolaires.

Méthodologie

   Pour réaliser notre étude, nous avons analysé les documents de référence du concours et les listes des participants au concours et les listes des prix par édition. Nous avons choisi de travailler sur toutes les productions primées en mathématiques de 2005 à 2011.

Analyse des résultats et discussion

   L'analyse des listes des participants et des gagnants au concours des enseignants innovants nous montre qu'un nombre important de produits multimédia est conçu par des enseignants innovants de toutes les disciplines exerçant au primaire, au collège et au lycée. Nous notons aussi la participation des seize académies régionales du Royaume à ce concours.

   Nous constatons aussi que beaucoup de ressources primées en mathématiques traitent la géométrie spatiale et dynamique, ceci montre que les enseignants de mathématiques sont conscients de l'utilité de la géométrie dans l'enseignement des mathématiques et d'autres disciplines scientifiques.

Tableau 1 : Nombre de prix par discipline

   L'analyse des donnés de ce tableau montre que les enseignants des différentes disciplines ont gagné ce concours et que les enseignants de mathématiques sont plus primés que les autres enseignants durant la période 2005-2011.

Dans la suite de l'article, nous analysons seulement les 12 prix en mathématiques.

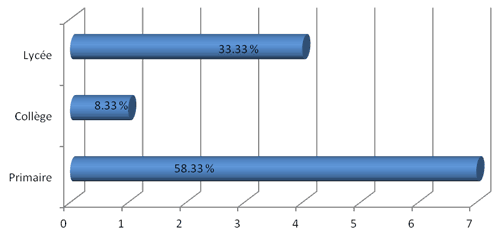
Figure 1 : Nombre de prix par niveau

   Ces résultats montrent qu'un pourcentage élevé des enseignants du primaire a innové en mathématiques et a gagné le concours des enseignants innovants.

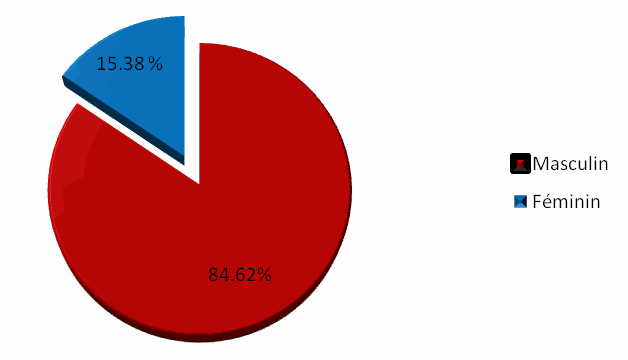
Figure 2 : Nombre de prix par sexe

   Selon la figure 2, nous voyons clairement que la majorité des enseignants innovants primés en mathématiques sont de sexe masculin (84.6 2%).

3-Nombre de prix type

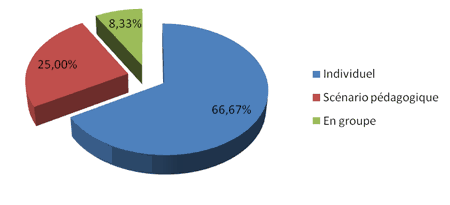
Figure 3 : Nombre de prix par type

   Nous constatons qu'un seul produit primé est conçu par un groupe d'enseignants, tandis que les autres sont conçus individuellement. Le travail en groupe est insuffisant par rapport au travail individuel. Nous signalons aussi une proportion importante de scénarios pédagogiques parmi les produits gagnants (25 %).

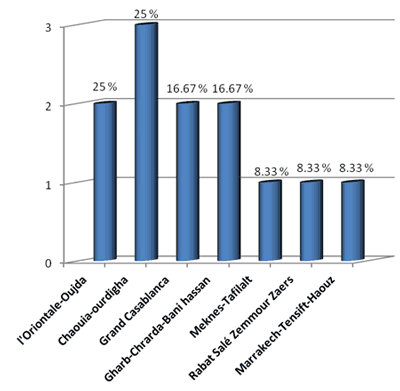
Figure 4 : Nombre de prix par région

   Certaines Académies ont une part importante de prix en mathématiques que les autres (Chaouia-ourdigha).

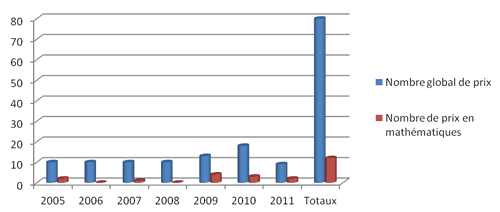
Figure 5 : Nombre de prix par année

   Nous enregistrons que l'année 2009 a connu un grand nombre d'enseignants innovants en mathématiques (4 prix). Les deux années 2006 et 2008 ont connu une absence des produits primés en mathématiques. Nous concluons aussi que les enseignants de mathématiques ont remporté la plus grande quantité des prix durant la période 2005-2011 (15 % des prix).

Conclusion

   Dans cette étude, nous avons montré que les enseignants de mathématiques sont plus primés que les autres enseignants, et que la plupart des lauréats du concours exercent dans l'enseignement primaire. Le travail en groupe est quasi absent des productions multimédias en mathématiques. On ce qui concerne les projets en mathématiques, les contributions des enseignants (84,62 %) sont plus élevées que celles des enseignantes (15,38 %)

   Nous avons aussi constaté que les enseignants ont une volonté pour surmonter les difficultés d'enseignement et d'apprentissage des mathématiques et redonner du sens à ses concepts. D'où la nécessité de valoriser la capacité d'innovation de nos enseignants et d'indexer les ressources numériques primées pour aider les enseignants à repérer facilement ces ressources. Cette indexation selon Robert Bibeau est très importante pour partager, diffuser et améliorer l'existant. « Une fois indexé selon les normes internationales ces ressources numériques seront plus facilement partagées, retrouvées et réutilisées. Chaque auteur ou éditeur pourra ainsi concentrer ses efforts et ses ressources pour développer l'aspect original et inédit de son oeuvre en prenant bien soin de l'arrimer aux outils et aux services déjà disponibles sur la toile » (Bibeau, 2005).

Recommandations

   Ces conclusions contribuent à la formulation des recommandations suivantes qui ont pour but d'améliorer cette expérience des enseignants innovants au Maroc et encourager les enseignants de mathématiques à participer massivement à ce concours pour diminuer le taux d'échec en mathématiques et redonner du sens à ses concepts :

• Améliorer, diversifier et certifier la formation des enseignants aux TIC.

• Encourager les enseignants de mathématiques à utiliser, partager et développer des productions numériques.

• Encourager la production des scénarios pédagogiques et produits multimédias en groupe.

• Encourager les enseignants innovants en mathématiques pour palier aux difficultés d'enseignement-apprentissage de cette discipline.

• Encourager l'innovation des ressources qui traitent les concepts qui posent problème lors du processus enseignement-apprentissage

• Organiser des rencontres régionales et nationales des enseignants de mathématiques pour la diffusion et l'échange des projets primés et pour encourager l'innovation pédagogique.

• Mettre à la disposition des enseignants une banque de ressources numériques primées.

Nachit Brahim^a,b,d,
Lablidi Ahmed^b,c,
Namir Abdelwahed^a,
Bahra Mohamed^d
Talbi Mohammed^b

a. Laboratoire de Technologie de l'Information et Modélisation(LTIM), Université Hassan II-Mohammedia, Casablanca, Maroc

b. Observatoire de Recherches en Didactique et Pédagogie Universitaire (ORDIPU), Université Hassan II- Mohammedia, Casablanca, Maroc

c. Centre Nationnal des Innovations Pédagogiques et d'Epérimentation TVI. Av. Mehdi Ben Barka. Souissi.1200 Rabat.

d. Cellule d'Observation et de Recherche en Enseignement des Sciences et Techniques (COREST), Centre Régional des Métiers de l'Education et de la Formation Derb Ghalef, Casablanca, Maroc

Cette contribution est sous licence Creative Commons (selon la juridiction française = Paternité - Pas de Modification) <http://creativecommons.org/licenses/by-nd/2.0/fr/>.

Bibliographie

Belli, T. et Pech E. (2006). Rapport au savoir en mathématiques. Mémoire professionnel, Institut Universitaire de Formation des Maîtres De l'académie d'Aix-Marseille Site d'Aix-en-Provence,
http://peysseri.perso.neuf.fr/PE2005/GFP05/MEMO2006/N.pdf

Bibeau, R.(2005). Les TIC à l'école : proposition de taxonomie et analyse des obstacles à leur intégration. Epinet n° 79 association EPI,
http://www.epi.asso.fr/revue/articles/a00511a. htm

Chevallard, Y. (1989). Arithmétique, algèbre, modélisation : Étapes d'une recherche. IREM d'Aix-Marseille, n° 16.

Couillard, P.(2004). Six compétences à développer,
http://recitmst.qc.ca/maths/Six-competences-a-developper

Commission européenne. (2007). L'enseignement scientifique aujourd'hui : une pédagogie renouvelée pour l'avenir de l'Europe. Luxembourg : Office des publications officielles des communautés européennes, 22 p.

Gueudet, G. & Trouche, L. (2009). Towards new documentation systems for mathematics teachers. Educational Studies in Mathematics, vol. 71, n° 3, p. 199-218, -

Hoyles, C., Lagrange J.-B. (dir. publ.). (2009). Mathematics Education and Technology – Rethinking the Terrain. New York : Springer Verlag,

Kuntz ,G. (2007). Des mathématiques en ligne pour renouveler l'enseignement des mathématiques ? Repère IREM n° 66 janvier.

Lafortune, L. (1997). Dimension affective en mathématiques. Bruxelles : De Boeck.

Rosar, D., Van Nieuwenhoven, C., Jonnaert, Ph. (2001). Les fractions, comment mieux comprendre les difficultés rencontrées par les élèves. Instantanés mathématiques, 32(2), p. 4-16.