Le problème du Grand-Duc

Alain Busser, Hilaire Fernandes
 

Contexte

   Lorsque Cosme II de Médicis [1] était élève, il pausait des questions déroutantes à son prof Galilée [2], comme tout lycéen digne de ce nom. Mais au lieu de demander « à quoi ça sert les maths ? » ou « pourquoi 2+2 font-ils 4 ? », il lui a posé la question suivante :

« Comment se fait-il que lorsqu'on lance 3 dés, le 10 sorte plus souvent que le 9 alors qu'il y a autant de manières d'écrire 10 que 9 comme somme de nombres allant de 1 à 6 ? »

   Comme quoi, au début du 17^e siècle, les lycéens passaient déjà plus de temps à jouer à des jeux de hasard, qu'à faire leurs devoirs...

   Il y a bien 6 manières d'avoir 9 et 6 manières d'avoir 10 :

   On va donc faire comme le Grand-Duc de Toscane (jouer aux dés), puis comme Galilée (calculer les probabilités). Ce qui est l'occasion d'explorer les blocs et collections de Smalltalk.

Simulation

Lancer un dé

   Pour lancer un dé, on doit commencer par en fabriquer un (dans un workspace). Dans le monde virtuel de DrGeo, cela se fait en choisissant au hasard un nombre entre 1 et 6 :

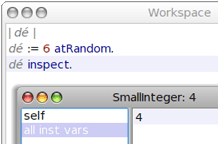
   En lançant l'inspecteur sur ce dé, on constate que c'est un petit entier, et il peut donc être additionné à d'autres entiers, comme par exemple des résultats d'autres lancers de dés.

Lancer trois dés

   Pour lancer trois dés, il suffit donc d'additionner trois dés :

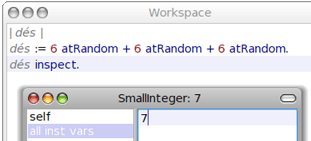
   Le résultat est stocké dans un entier UnJeu.

Jouer dix fois

   Pour jouer 10 fois, on a besoin d'un tableau (appelé histoire) où stocker les résultats des 10 jeux. On a également besoin d'un indice n pour parcourir le tableau :

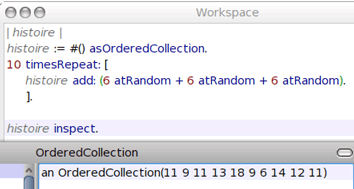
Statistiques

   Il suffit maintenant de quelques modifications pour faire des statistiques sur les résultats des lancers de dés. Au lieu d'un tableau histoire donnant l'historique des parties jouées, on prend un tableau stats qui contient les statistiques du jeu. On doit initialiser ce tableau pour qu'il ne contienne que des zéros puis, pour chaque résultat possible, compter combien de fois il est sorti et mettre le résultat dans le tableau.

Tableau d'effectifs

   On en profite pour rendre la variable UnJeu locale :

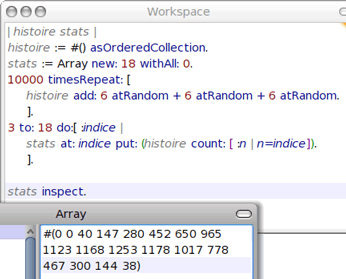
   Le début du tableau est formé de 0 parce que ni le 1 ni le 2 ne sont jamais sortis (essayez de faire un 2 en lançant 3 dés!) :

   Dans ce cas, le 9 est sorti 1123 fois, et le 10 sorti 1168 fois. Le Grand-Duc de Toscane aurait-il eu raison ?

Diagramme en bâtons

   Comme il faut un temps très bref pour lancer les dés 1 000 fois, autant les lancer 10 000 fois ; et en profiter pour dessiner les effectifs. Les dessiner, ça veut dire faire des traits sur une feuille blanche, bref, une variable appelée feuille. C'est un objet de type DrGeoCanvas (une figure DrGeo) qu'on crée simplement en lui envoyant le message new! Un autre objet sera utile, un objet graphique (le trait par exemple) qu'on va déposer sur la feuille ; on devrait donc l'appeler décalcomanie mais on lui préfèrera trait parce que c'est plus court à écrire.

Point

   L'origine du segment à tracer est un point de coordonnées 0 et n (indice du point). On crée et dessine ce point en envoyant à la feuille un message point assorti des coordonnées du point. Puis on envoie à l'origine une suite de messages disant :

1. Sois pas timide, montre-toi! (show) ;
2. Fais-toi une tête au carré! (square) ;
3. Maquille-toi en bleu (color: Color blue) ;
4. rebaptise-toi en n (name: n asString).

   Le tout s'écrit origine show ; square ; color : Color blue ; name: n asString.

Segment

   Les coordonnées de l'origine du segment sont 0 et n. Celles de son extrémité sont 0 et l'élément du tableau d'indice n (divisé par 100 pour rentrer dans le dessin).

   La syntaxe est feuille segment: origine to: indice@((histoire count: [ :n | n=indice])/100)

Dessin

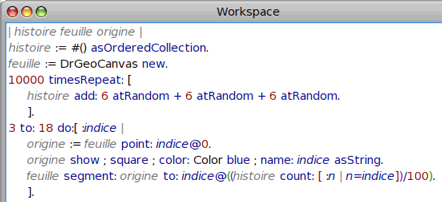
   Le script de dessin est celui-ci :

   Avec la coloration syntaxique :

Résultat

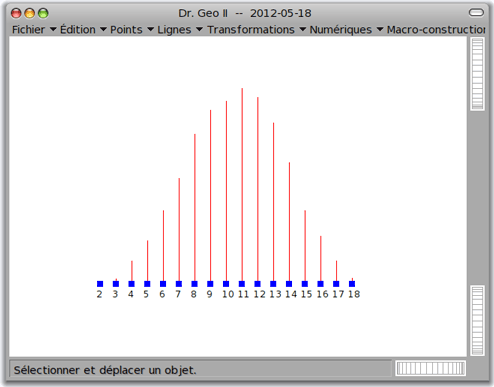
   Il semble que finalement, le Grand-Duc ait eu raison (à l'époque il valait mieux éviter de dire le contraire, à moins d'être roi...) : Le 9 sort vraiment moins souvent que le 10.

Théorie

   La probabilité d'un évènement est le quotient du nombre de cas favorables à l'évènement, par le nombre de cas possibles.

Dénominateur

   Le nombre de cas possibles est égal à 6×6×6=216. C'est donc par ce nombre qu'il faut diviser les nombres qu'on trouvera ensuite. On peut faire le comptage par Smalltalk en construisant une liste et en comptant ses éléments. Autant appeler cette liste liste, et en faire une OrderedCollection (de taille variable, contrairement au tableau dont la taille est déterminée lors de sa création). On appelle a, b et c les résultats que peuvent prendre les trois dés. Alors pour toutes valeurs de a, b et c allant de 1 à 6, on ajoute à la liste la somme a+b+c :

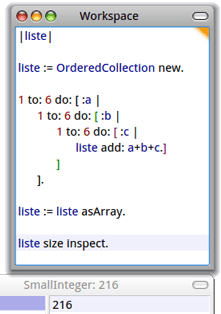
   Ensuite, pour préparer la suite, on retransforme liste en tableau, en le lui demandant par asArray ; puis on affiche la valeur de la taille de ce tableau : 216.

Numérateur

   Pour savoir quel nombre on doit diviser par 216, il suffit de sélectionner parmi les 216 nombres du tableau liste, ceux qui valent 9, de stocker le résultat dans une variable favorables et de compter le nombre de « 9 » qu'il y a dans cette variable :

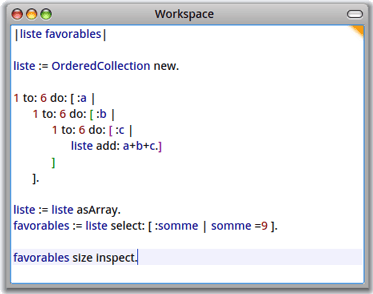
   On trouve 25, ce qui veut dire que la probabilité d'avoir 9 est 25/216=0,1157 environ. On peut calculer cette probabilité sous forme de fraction irréductible :

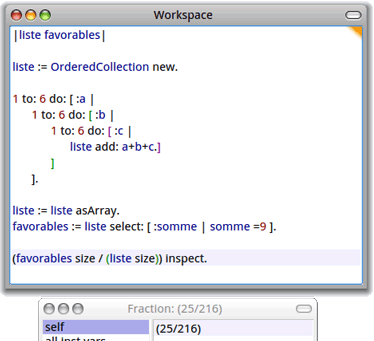
   On peut aussi lui envoyer le message asFloat pour avoir une valeur approchée.

   La probabilité d'avoir 10 se calcule de manière similaire, en remplaçant le 9 ci-dessus par un 10. On trouve 1/8=0,125 soit légèrement plus que la probabilité d'avoir 9 : Le Grand-Duc de Toscane avait raison. Mais c'était quand même un vilain garçon qui aurait mieux fait d'apprendre ses leçons au lieu de jouer aux dés pendant des heures.

Alain Busser
Enseignant de mathématiques,
animateur à l'IREM de l'île de la Réunion

Hilaire Fernandes
Enseignant de mathématiques,
Dr en informatique

NOTES

[1] http://fr.wikipedia.org/wiki/Cosme_II_de_Médicis

[2] http://fr.wikipedia.org/Galileo_Galilei