|
De l'algorithme de Didon à la spirale d'Ulam
Alain Busser, Hilaire Fernandes
Jardin zen
Un robot est chargé de parcourir un terrain, pas à pas, en entier, en se limitant aux points à coordonnées entières, mais en ne parcourant chacun qu'une fois et en les parcourant tous. Une courbe de Peano est un algorithme permettant de réaliser cette tâche, mais l'algorithme est un peu difficile à mettre en oeuvre à moins d'utiliser les RegExp qui ne sont pas au programme (ce qui est dommage !).
Ce problème n'est pas uniquement théorique puisqu'il permet de réduire d'une dimension un problème bidimensionnel. La légende dit que pour fonder le royaume de Carthage, Didon [1], à qui les autochtones n'avaient accordé que la surface qui tient dans une peau de boeuf, a découpé celle-ci en une fine lanière qui a pu encercler tout Carthage. La méthode pour parcourir un jardin zen [2] en spiralant [3], sera donc ici appelée algorithme de Didon...
Dessin de la spirale
On peut donc demander au robot de tracer une spirale en partant du centre de la figure, avec l'algorithme suivant :
- initialiser ample (une variable donnant le nombre de pas à effectuer dans la direction courante) à 1 ;
- faire ample pas vers la droite ;
- faire ample pas vers le haut ;
- incrémenter ample (pour ne pas repasser ultérieurement par un point déjà parcouru)
- faire ample pas vers la gauche ;
- faire ample pas vers le bas ;
- incrémenter à nouveau ample ;
- revenir au point 2.
En créant une figure DrGeoII en Smalltalk, on peut afficher le nombre de pas effectués (numero ci-dessous) et la traduction de l'algorithme ci-dessus en Smalltalk peut ressembler à ceci (la première ligne donne les variables dont x et y sont les coordonnées courantes du robot, et spirale est une variable contenant la figure, ou DrGeoCanvas) :
Pour commencer, on crée les variables dont on aura besoin et on les initialise :
| numero ample x y spirale tamponne|
x := y := numero := ample := 0.
tamponne := [
numero := numero + 1.
(spirale point: x@y) square ; name: numero].
spirale := DrGeoCanvas new.
tamponne value.
10 timesRepeat: [
ample := ample + 1.
ample timesRepeat: [
x := x + 1.
tamponne value].
ample timesRepeat: [
y := y + 1.
tamponne value].
ample := ample + 1.
ample timesRepeat: [
x := x - 1.
tamponne value].
ample timesRepeat: [
y := y - 1.
tamponne value]]
|
Grâce au bloc Smalltalk tamponne, après avoir fait chaque pas, le robot dépose un point par terre en le numérotant (un peu comme une machine de Turing). Pour copier-coller facilement le script ci-dessus, on peut le télécharger ici : Ulam0.txt
Pour tester cet algorithme, on doit fermer la figure DrGeo, et sur le plan de travail d'une blancheur immaculée, un clic permet d'ouvrir un workspace :
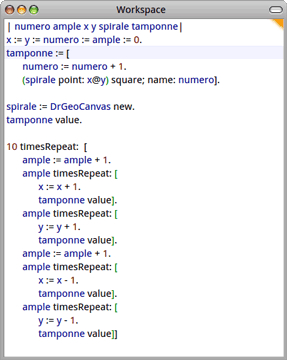
Puis d'y entrer (ou copier-coller) le script ci-dessus, ce qui, avec la belle coloration syntaxique de DrGeoII, ressemble à ceci :
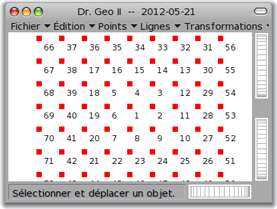
Ensuite, pour exécuter le script, on sélectionne tout (par Alt-A comme all), puis on l'exécute par doIt (soit par clic-droit suivi du choix de doIt dans le menu contextuel, soit par Alt-D) ; ce qui a pour effet de créer une figure DrGeoII qui se remplit de points numérotés en spirale :
De la spirale à Ulam
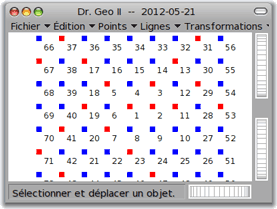
Maintenant, comme Stanislaw Ulam [4], on peut changer la couleur d'un point selon que son numéro soit premier ou composé, puisque DrGeoII gère les nombres premiers. Pour cela il suffit d'ajouter dans le coup de tampon une coloration en bleu si le nombre n'est pas premier :

Le script devient alors : Ulam1.txt. Et la figure devient :
Cerise sur le gâteau : Il suffit maintenant de ne pas représenter du tout les nombres composés pour avoir une spirale d'Ulam ; dans le bloc tamponne vu précédemment, on met :
|
numero isPrime ifTrue: [(spirale point: x@y) square ; name: numero]
|
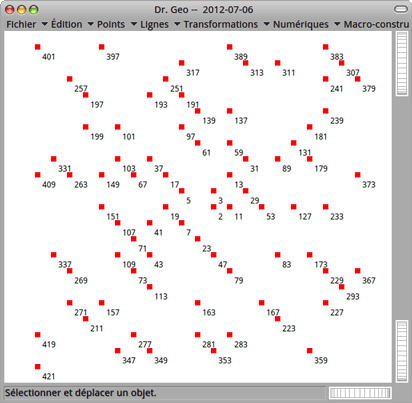
Le script pour la spirale d'Ulam est ici : Ulam2.txt. Avec la coloration syntaxique :
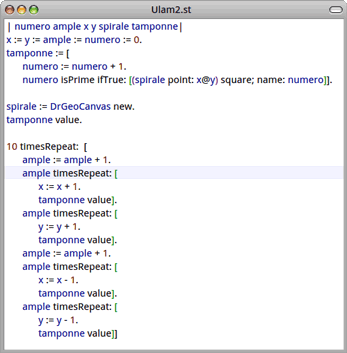
Il dessine la figure suivante (à zoomer pour mieux l'interpréter) :
Fast zen
L'algorithme de Didon permet d'aborder la notion d'algorithmique [5], puisqu'il est intuitivement évident que le temps qu'il va prendre dépend du nombre de boucles à effectuer (il faut plus de temps pour faire 1 000 boucles que pour n'en faire qu'une). DrGeoII peut facilement mesurer le temps, en enfermant l'algorithme de Didon entre crochets, pour en faire un bloc Smalltalk, et en envoyant à ce bloc le message timeToRun, qui, après le choix de print, affiche, en millisecondes, le temps qu'a pris le parcours de la spirale. On obtient un résultat de ce genre :
|
nombre de boucles |
temps (millisecondes) |
|
0 |
94 |
|
1 |
124 |
|
2 |
160 |
|
3 |
218 |
|
4 |
292 |
|
5 |
362 |
|
6 |
472 |
|
7 |
582 |
|
8 |
698 |
|
9 |
850 |
|
10 |
1018 |
On peut alors se demander comment le temps dépend du nombre de boucles effectuées. Le logiciel ImageJ suggère que la dépendance est du quatrième degré :
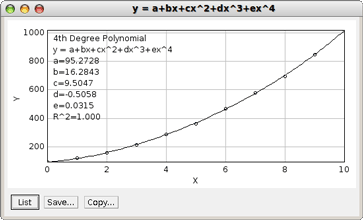
Reste alors à trouver une théorie qui peut expliquer cela (le même ImageJ suggère que le temps mis à dessiner n points est fonction affine de n, avec environ 82,417 millisecondes par point, et 1,85 milliseconde pour démarrer le script)...
Alain Busser
Enseignant de mathématiques,
animateur à l'IREM de l'île de la Réunion
Hilaire Fernandes
Enseignant de mathématiques,
Dr en informatique
NOTES
[1] Didon :
http://fr.wikipedia.org/wiki/Didon
[2] Zen Puzzle Garden (en anglais) :
http://www.lexaloffle.com/zen.php
[3] Spirale d'Ulam :
http://fr.wikipedia.org/wiki/Spirale_d%27Ulam
[4] Stanislaw Ulam :
http://fr.wikipedia.org/wiki/Stanislaw_Marcin_Ulam
[5] Théorie de la complexité (informatique théorique) :
http://fr.wikipedia.org/wiki/Théorie_de_la_complexité_des_algorithmes
|