Représentation des objets en machine
Codage des couleurs et des entiers

Alain Busser, Hilaire Fernandes
 

   Comme on l'a vu précédemment, les capacités d'introspection de DrGeoII permettent d'utiliser ce dernier pour étudier (voir, ou modifier à titre expérimental) la machine virtuelle Smalltalk sur laquelle il tourne.

Définition : Une machine virtuelle, c'est une machine, à ceci près qu'elle est virtuelle !

1. Par machine il faut penser simulation d'un ordinateur, et c'est donc une machine au sens de machine de Turing à ceci près que contrairement à la machine de Turing, Smalltalk a une quantité de mémoire limitée (qu'on peut connaître en utilisant le profileur, qui affiche la quantité de mémoire utilisée, et la quantité totale disponible).

2. Par virtuelle il faut juste comprendre qu'on n'a pas besoin du tournevis ni du fer à souder pour réparer, ou juste pour disséquer : Aucune machine virtuelle Smalltalk n'a été maltraitée pendant l'écriture de ces articles (du moins de manière pérenne, il suffit de ne pas enregistrer les modifications à la fermeture du fichier pour annuler celles-ci) !

   Dans cet article, on va voir comment sont représentés les couleurs et les nombres entiers dans DrGeoII. On va le faire dans un Workspace et non dans une figure DrGeoII.

 
Représentation interne des couleurs

   En explorant les primitives graphiques de Smalltalk avec un browser [1], on découvre qu'il est possible d'additionner des couleurs :

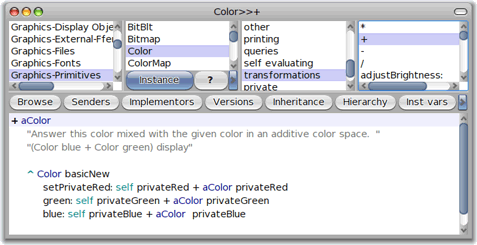
   L'algorithme n'est d'ailleurs pas compliqué : On se contente d'additionner les composantes rouge, verte et bleue des deux couleurs. Pour voir ce que ça donne, on peut ouvrir un Workspace pour y écrire, et tester, un petit programme en Smalltalk :

   Le programme consiste par exemple à additionner du bleu avec du rouge :

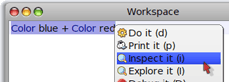
   Si on choisit DoIt pour exécuter le programme, on ne verra rien, parce qu'on n'a pas demandé explicitement au programme d'afficher le résultat. Alors on peut choisir PrintIt ou, comme ci-dessus, InspectIt pour voir non seulement la couleur résultante, mais aussi toutes ses propriétés. Le résultat est quelque peu surprenant :

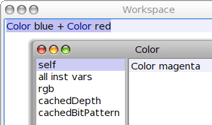
   Un bon exercice de hacking, c'est de regarder comment DrGeoII « sait » qu'en mélangeant du rouge avec du bleu, on obtient du magenta (on peut utiliser le browser, ou essayer comment d'autres combinaisons de couleurs s'affichent). Ci-dessous, on reverra ce simulacre d'intelligence à l'oeuvre avec les nombres. Les durées aussi s'additionnent de manière très instructive.

   Plus bas dans la fenêtre de l'inspecteur, on aperçoit une méthode appelée rgb (comme red-green-blue) ; on imagine qu'elle retourne les quantités de rouge, vert et bleu qu'il y a dans le magenta, et comme on sait que la quantité de vert est nulle, on peut espérer voir comment la couleur magenta est codée en Smalltalk ; mais il y a comme un problème là :

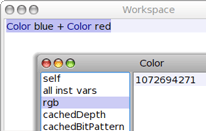
   Pour retrouver ce nombre dans le Workspace (afin de chercher sa représentation interne), on peut utiliser la méthode privateRGB :

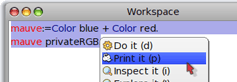
   Si on imprime le nombre, on retrouve celui de l'inspecteur :

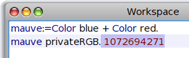
   L'inspecteur, là-dessus, il est perplexe à nouveau : Il croit à un code secret avec tous ces chiffres! Mais la méthode asWords des nombres entiers permet de l'afficher tout autrement :

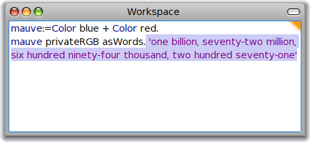
   Le code du magenta est donc un milliard soixante douze millions six cents quatre-vingt quatorze mille deux cents soixante et onze ! De même, on peut afficher les nombres entiers en chiffres romains. Ce qui a l'avantage de montrer l'intérêt des représentations multiples d'un objet (ici un nombre) et par une question quelle est la vraie représentation ? de suggérer l'existence d'une représentation particulière : La représentation interne en machine. Celle-ci, on s'en doute, est binaire. Pour l'afficher avec concision, on peut l'afficher en hexadécimal avec la méthode hex :

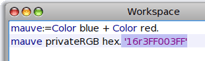
   On distingue aisément trois octets : Le rouge et le bleu sont égaux à 3FF (soit 1111111111 en binaire, ou 1023 en décimal) et le vert est égal à 0.

   On peut vérifier avec d'autres couleurs :

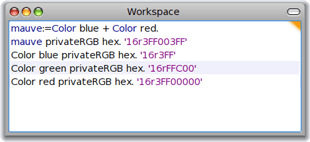
   Par exemple, le vert est égal à FFC00 en hexadécimal, soit 11111111110000000000 en binaire. Ce qui confirme que chaque composante rouge-vert-bleu est codée par un nombre entier sur 10 bits, soit 30 bits en tout ; le 1023 représentant la quantité maximale possible, et le 0 représentant l'absence totale de la couleur.

   Tout ceci est bien utile pour les utilisateurs daltoniens de DrGeoII, mais pour les autres, il suffit, au lieu d'inspecter une couleur, de l'explorer :

   Ce qui, en plus des informations précédentes, donne un aperçu de la couleur :

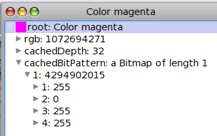
   Du coup, on peut se demander quel est l'avantage de DrGeoII sur Pharo Smalltalk : On peut, avec ce genre de manipulation, créer des objets de couleurs non existantes dans DrGeoII, par exemple la moitié du magenta :

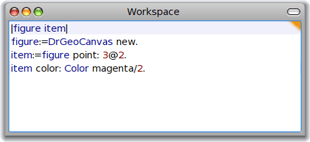
   Cette fois-ci, le script n'a pas à être inspecté ni imprimé, mais seulement exécuté, avec doIt ; ce qui donne ceci :

 
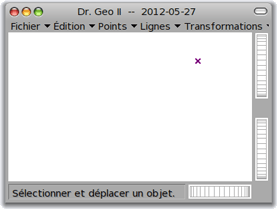
Représentation interne des nombres

   En browsant les nombres, on peut voir aussi comment eux sont représentés dans la machine virtuelle Smalltalk. Pour les nombres réels (float) on retrouve les notions de mantisse et exposant, et on voit comment les calculs sont effectués à partir des mantisses et exposants des opérandes. Avec les entiers, on a un aperçu de la manière dont les calculs sont effectués à partir des bits qui constituent ces entiers.

   Pour commencer, la factorielle est souvent calculée récursivement ; Smalltalk n'échappe pas à cette règle :

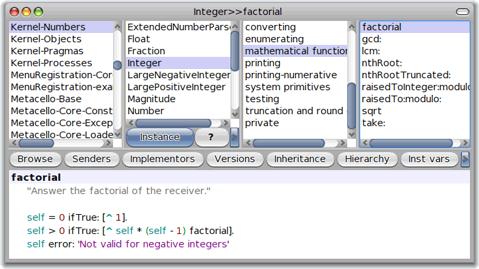
   L'addition de deux entiers (qu'on appellera respectivement self et aNumber pour préserver leur anonymat) se fait

1. en regardant si aNumber (le second opérande) est bien entier ;
2. si c'est le cas, en regardant si les deux opérandes sont du même signe :
   1. si oui, on les additionne binairement,
   2. sinon, on soustrait leurs valeurs absolues.

en Smalltalk ça donne ceci :

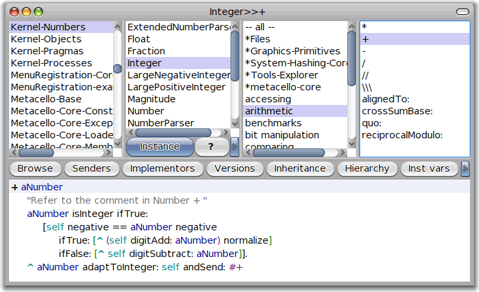
   Ce qui n'explique finalement pas grand-chose, il reste à voir comment les nombres sont additionnés binairement :

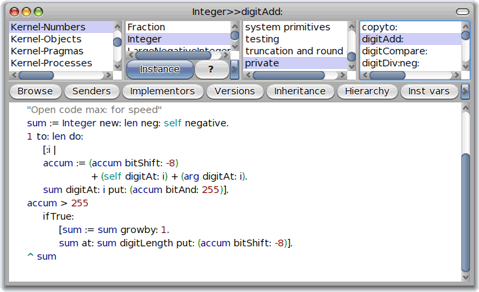
   Cette fois-ci, les deux nombres à additionner ont len chiffres (abréviation de length) ; et ils s'appellent self et arg, et sont interprétés comme des tableaux d'octets. Le numéro du chiffre (en base 256) qu'on calcule est i, et la retenue (un octet) est accum. Alors

1. on décale la retenue de 8 chiffres binaires vers la gauche (pour l'additionner au chiffre suivant)

2. on additionne la retenue avec les chiffres (des octets) numéros i des deux opérandes ; le résultat peut faire plus d'un octet (à cause d'une éventuelle retenue). Le chiffre à placer dans la somme est formé des 8 derniers chiffres binaires de accum, et on les récupère avec un et binaire avec 255, qui annule les chiffres autres que les 8 derniers, qui eux, sont inchangés.

3. le reste se passe uniquement s'il y a une retenue à la fin (accum supérieur à 255) : On rajoute un chiffre à la somme, obtenu en décalant une dernière fois les chiffres de accum.

   Par contre, on ne peut pas aller plus loin, parce que l'addition des octets se fait en interne, et le code est inaccessible à Smalltalk.

   Pour finir, l'algorithme de calcul de la racine carrée entière est assez surprenant :

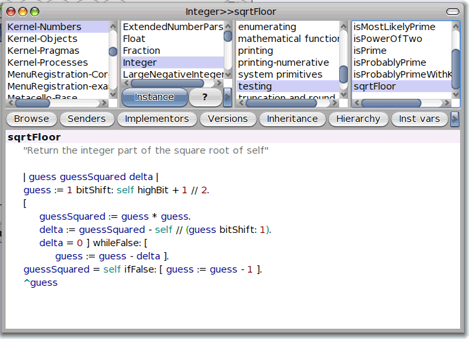
   Qui saurait deviner ce que fait cet algorithme, s'il n'y avait pas les deux premières lignes ?

Alain Busser
Enseignant de mathématiques,
animateur à l'IREM de l'île de la Réunion

Hilaire Fernandes
Enseignant de mathématiques,
D^r en informatique

NOTE

[1] Voir « Hacking de Dr Geo avec Dr Geo », Alain Busser, Hilaire Fernandes
http://www.epi.asso.fr/revue/articles/a1209b.htm