Géométrie interactive et programmation

Alain Busser, Hilaire Fernandes
 

   À la confluence de la géométrie euclidienne et analytique, la programmation permet de traiter, de modéliser des situations mathématiques pédagogiquement intéressantes. Pour peu de disposer d'un environnement convivial de programmation interactive, inscrit dans un micro-monde de géométrie dynamique, l'approche est amusante et suffisamment récréative pour susciter l'intérêt chez les élèves. Son inscription dans le cadre du nouvel enseignement de spécialité de terminal Informatique et Science du Numérique [1] est prometteuse, nous l'illustrerons d'exemples dans nos prochains articles ; dans le présent texte nous vous proposons de découvrir ce qui se cache derrière « Géométrie interactive et programmation ».

   L'apparition de la programmation dans une figure géométrique prend essentiellement deux formes : les scripts et les figures programmées. Dr. Geo [2] fût un des premiers logiciels à proposer cette approche duale de la programmation dans un micro-monde de géométrie dynamique.

   Une des particularités de Dr. Geo est d'être écrit avec le même langage informatique utilisé pour l'écriture des scripts et des figures programmées, à savoir Smalltalk [3] et son implémentation libre Pharo soutenue par l'INRIA [4].

   En anglais, le terme Smalltalk signifie babillage, jargon de petit enfant. En effet, Alan Kay [5], le principal architecte du langage Smalltalk, conçut celui-ci dans la perspective d'une utilisation par des enfants. Le babillage auquel il est fait allusion est le flot incessant de messages que s'envoient les objets entre eux.

   Cet exemple illustre du code Smalltalk proche du langage naturel. Pour peu de créer les objets et les méthodes nécessaires, ce code est valide :

preparation := Recette new. preparation ajoute: 200 g de: Sucre. preparation ajoute: 200 g de: Farine. preparation ajoute: 20 g de: Levure. preparation ajoute: 3 de: Oeuf. preparation melange. preparation cuisson: 45 minutes

   Nous écrivons aussi des expressions comme :

90 secondes + 30 secondes

qui retourne un objet durée de 2 minutes.

   En mélangeant les unités cela marche tout aussi bien :

2 minutes + 90 secondes

cela nous retourne une durée de 3 minutes et 30 secondes.

Nous testons des durées :

t > 5 minutes if True: ['faire quelque chose'].

   Comment ce tour de force est-il possible ? En quatre mots : no type, pure object. L'objet de cet article n'étant pas Smalltalk, nous invitons le lecteur curieux vers des ouvrages spécialisés comme Pharo par l'exemple [6].

   Autre particularité de Dr. Geo, il est modifiable depuis lui même. Il est modifiable depuis lui-même veut dire qu'il y a un entrelacement fort entre le code source et son code compilé d'une part et que les outils nécessaires à son étude et sa modification sont présents d'autre part.

   La capture écran suivante de l'environnement Dr. Geo montre une figure géométrique interactive avec un exemple de symétrie axiale, le menu de l'environnement donnant accès aux outils orientés programmation et enfin une vue du navigateur de code source. Ce dernier affiche la méthode update de l'objet milieu de deux points ; elle est responsable de la mise à jour du point milieu selon la position de ses deux points parents.

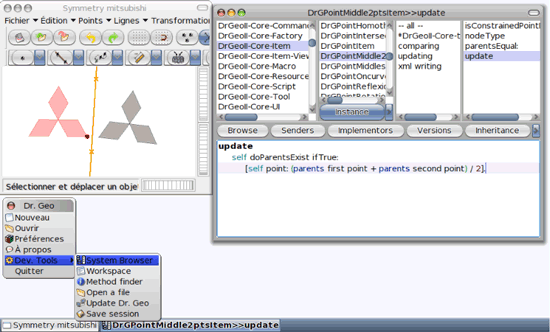
   Ainsi, si le code source de Dr. Geo s'étudie depuis lui-même avec le navigateur de code, il est – depuis ce même outil – modifiable et compilable, ceci même avec des figures géométriques présentes dans l'environnement. Nous comprenons alors que l'accès et l'étude du code source occupent une place importante dans Dr. Geo, comme c'est le cas dans les métiers de l'informatique : savoir étudier un code source en constitue une composante importante, à haute valeur ajoutée. C'est un peu comme si, dans une auto-école, des cours de mécanique (facultatifs) étaient dispensés en plus des cours de conduite, qui permettraient aux futurs conducteurs de tout savoir sur le fonctionnement de leur véhicule, en plus de savoir l'utiliser : l'enfant est utilisateur du logiciel mais aussi un potentiel concepteur.

   De ces courtes explications de quelques particularités de Dr. Geo, le lecteur comprendra que les scripts et les figures programmées constituent des éléments de premier ordre – et non des pièces rapportées – ayant pleinement accès aux arcanes du logiciel, à savoir ses objets et ses méthodes, sans aucune limitation.

Scripts et figure interactive

   Les scripts sont des bouts de programmes incrustés dans une figure. Ces scripts étendent les possibilités des logiciels de géométrie interactive par des manipulations et des calculs non planifiés par leurs auteurs. Une API spécifique ou non donne accès aux méthodes des objets géométriques de la figure, le script opère un traitement sur ceux-ci et retourne vers la figure une valeur (au sens informatique), valeur ensuite réutilisable par d'autres objets, y compris des scripts. Dans Dr. Geo, une API spécifique est inutile, les scripts sont des méthodes ayant un accès complet aux méthodes des objets géométriques de Dr. Geo, ainsi qu'aux méthodes de tous les objets de Smalltalk.

   Le script ci-dessous illustre le calcul de la pente d'une fonction en une abscisse d'un point.

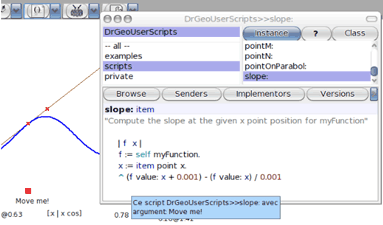
   Un script se comporte donc comme un objet d'une figure géométrique : il est défini à la fois par ses arguments – des objets que l'utilisateur choisit dans la figure – et par le traitement qu'il effectue sur ceux-ci ; le résultat de ce traitement est ensuite affiché dans la figure et réutilisable comme argument par d'autres scripts ou objets géométriques.

Figures programmées

   Il s'agit de la description d'une figure géométrique exclusivement sous la forme d'un programme. A l'aide d'une API spécifique, l'utilisateur décrit de façon programmée sa figure. L'utilisation des spécificités d'un langage de programmation (structures de contrôle, bloc de code anonyme – fonction lambda) pour décrire une figure ouvre d'amusantes applications.

   Pour créer une figure simple, nous écrirons dans un éditeur de script (Workspace) le code suivant :

| figure a s | figure := DrGeoCanvas new. a := figure point: 0@0. s := figure segment: a to: 5@0. figure middleOf: s.

   Pour obtenir la figure interactive correspondante, nous sélectionnons le code par un [Alt]+a (ou [Ctrl] selon le système d'exploitation) puis le compilons/exécutons par un [Alt]+d (ou dans le menu contextuel de l'éditeur, choisir Do-it).

   L'intérêt des figures programmées est d'adjoindre les structures de contrôle et autres blocs de code. L'exemple ci-dessous illustre la distribution de 10 000 lancers d'une paire de dés. Le résultat correspond bien à notre attente de mathématiciens :

 
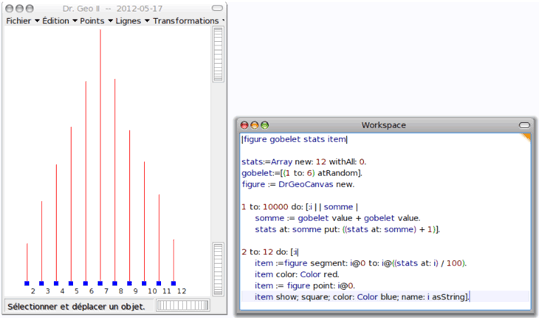
   Ce petit tour d'horizon est terminé, nous espérons qu'il aura aiguisé votre curiosité. Dans de prochains articles – toujours courts – nous présenterons des exemples d'utilisation pédagogique avec des élèves.

1. Inspection d'une figure géométrique
2. Codage des couleurs
3. Codage des nombres
4. Spirale d'Ulam
5. Chronométrie
6. Hacking du hashage SHA-5

Alain Busser
Enseignant de mathématiques,
animateur à l'IREM de l'île de la Réunion

Hilaire Fernandes
Enseignant de mathématiques, Dr. en informatique

NOTES

[1] « Enseignement de spécialité d'informatique et sciences du numérique, trois BOEN en octobre 2011 », rubrique Nous avons lu, EpiNet n° 128, oct. 2011.
http://www.epi.asso.fr/revue/lu/l1110k.htm

[2] Dr. Geo, be a geometer!
http://drgeo.eu/

[3] Wikipédia : Smalltalk.
http://fr.wikipedia.org/wiki/Smalltalk

[4] Pharo is a clean, innovative, open-source Smalltalk-inspired environment.
http://pharo.org/

[5] Wikipédia : Alan Kay.
http://fr.wikipedia.org/wiki/Alan_Kay

[6] Pharo par l'Exemple, livre en ligne (PDF) de Andrew Black, Stéphane Ducasse, Oscar Nierstrasz et Damien Pollet avec l'aide de Damien Cassou et Marcus Denker, traduit en français par Martial Boniou, René Mages et Serge Stinckwich, 368 pages, sous licence Creative Commons BY-SA.
http://pharobyexample.org/fr/index.html