Faire découvrir les nombres premiers.
En classe ou en groupe de travail,
à l'aide d'un logiciel

Alain Barnier
 

En, bref :
   Ce logiciel est gratuit et vous pouvez vous en servir librement.

   Il peut être utilisé sur tout PC 64 bits sous Windows.

   Il permet de calculer, d'observer, de compter et d'expérimenter commodément les nombres premiers et aussi de décomposer en facteurs premiers les nombres entiers.

   Tout ceci, évidemment, en tenant compte de certaines limites, assez grandes à notre échelle.

   Ses applications peuvent être adaptées à presque tous les niveaux : primaire, collège, lycée et ateliers de recherche.

Que fait-il ?
   Ce programme peut calculer et afficher tous les nombres premiers jusqu'à une valeur ou un rang donné.

   On peut choisir de n'afficher que le dernier ou le plus grand de ces nombres.

   Tous les nombres premiers sont affichés avec leur rang.

   On peut afficher des nombres premiers isolés déjà calculés ou des séquences de ceux-ci en les triant grâce à leurs rangs ou leurs valeurs.

   Dans une même session, vous pouvez calculer des nombres premiers et décomposer des nombres entiers quelconques.

   Les nombres premiers calculés sont mis en commun pour ces deux parties et mémorisés pour toute la session.

   Quand on ferme le programme, ils sont effacés.

   Une option permet d'afficher et de compter parmi les nombres déjà calculés, tous les couples consécutifs de différence fixée et qui sont compris entre 2 valeurs. On peut choisir de ne faire afficher que les occurrences où un nombre donné de solutions se suivent.

Ses limites :
   Dans la pratique, les limitations sont surtout dues au temps de calcul des grands nombres premiers.

   La présente version n'utilise que la mémoire vive de l'ordinateur.

   Elle est très « portable » et convient pour calculer très rapidement des nombres premiers jusqu'à des valeurs de 15 ou 20 millions et pour factoriser rapidement des nombres de 14 chiffres.

   Elle factorise aussi rapidement n'importe quel nombre ne comportant pas de facteurs de plus de 7 chiffres.

   D'autres versions existent et permettent de dépasser ses limites dues au temps de calcul, mais elles utilisent un fichier annexe avec une grande quantité de nombres premiers déjà calculés.

En théorie :
   Les nombres premiers doivent être inférieurs à (2^63-1).

   Soit environ : 9 000 000 000 000 000 000 = 9x10^18.

   Les nombres à factoriser peuvent être quelconques tant que leurs facteurs premiers ne dépassent pas (2^63-1) .

Quels élèves concernent-ils ?
   Son domaine pédagogique d'application concerne les classes de collège et de lycée et même au-delà. Peut-être également, le primaire pour des illustrations simples.

   Les applications comme vous le verrez dans les suggestions et exemples suivants peuvent être adaptées pour chaque niveau.

   On peut l'utiliser en atelier de recherche ou en club de mathématiques.

Quelques applications suggérées

Mais vous pouvez facilement en trouver d'autres.

1 - Expérimenter la recherche de nombres premiers pour de petites valeurs. Vérifier les résultats obtenus « à la main » . (Collège, lycée).

2 - Construire un algorithme permettant de calculer les nombres premiers jusqu'à une valeur ou un rang donné. Vous pouvez utiliser les vecteurs ou tableaux ou listes de votre langage. (Lycée et supérieur).

3 - Vérifier des décompositions en facteurs premiers faites « à la main » (Collège, lycée).

4 - Afficher tous les nombres premiers jusqu'à 100, 1000...

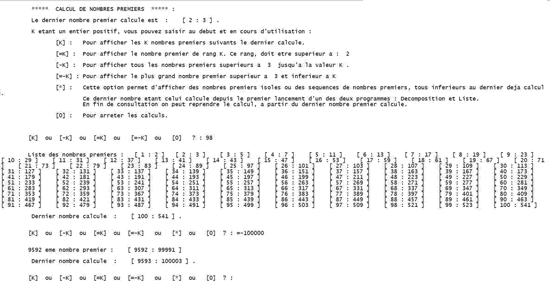
5 - Faire constater l'irrégularité de la répartition de ces nombres dans les listes obtenues. (Collège, lycée).

6 - Observer les répartitions et les effectifs de nombres premiers sur des intervalles variés de longueur constante ou non.

7 - Observer la variation de la densité des nombres premiers inférieurs à N, quand cette valeur augmente. Avec ce que vous avez constaté peut-on généraliser pour de plus grandes valeurs ?

8 - Vérifier que l'écart entre deux nombres premiers consécutifs peut être très grand, et qu'il a l'air de pouvoir être un multiple quelconque de 2 (sauf pour 2 et 3).

9 - Chercher à démontrer que l'écart entre deux nombres premiers consécutifs n'est pas limité. (Lycée - La démonstration ne fait appel qu'à de l'arithmétique basique et à la notion de factorielle).

Avec les nombres jumeaux et leur généralisation, plusieurs exercices possibles :

10 - Afficher tous les nombres jumeaux jusqu'à 100, 1 000... ou entre deux valeurs.

11 – Existe-t-il des nombres trijumeaux à part (3, 5, 7) ? Chercher une démonstration de la conjecture affirmant qu'il n'y en a pas (lycée, arithmétique basique simple).

On pourra démontrer au préalable : si 3 nombres se suivent avec des écarts égaux à 2, il y en a toujours un qui est un multiple de 3.

12 - Afficher tous les couples de nombres premiers consécutifs espacés d'une valeur donnée. Jusqu'à une certaine limite ou entre deux limites.

Question : Y a-t-il pour cette valeur des séquences de 4, 5, 6... nombres consécutifs régulièrement espacés ?

Recherches :

13 - Pour trois nombres premiers consécutifs espacés d'une même valeur, chercher des conditions sur cette valeur pour que ces trois nombres puissent exister.

Chercher à démontrer : cette valeur doit être un multiple de 6, à l'exception du triplet (3, 5, 7). (Lycée, arithmétique basique simple).

14 - Y a-t-il une limite à la longueur des séquences de nombres premiers constitutifs espacés d'une même valeur ?

   Chercher à démontrer : Une limite est 6 quand l'espace est de 6 et elle est de k*6 quand l'espace entre les nombres vaut k*6 (lycée, arithmétique basique simple). Mais II y a peut-être des limites inférieures !

   Les démonstrations ne font appel qu'à des notions d'arithmétique simples.

   Vous les trouverez sur la page Web consacrée à ce logiciel :

http://alainb-sites.fr/N-premiers/

   On y trouve aussi des liens vers des sites sur les nombres premiers et des exemples d'utilisation du logiciel.

   Et également des liens vers les pages Web d'autres logiciels à usages pédagogiques que je propose.

   Vous y verrez aussi une étude de mon ami et collègue Gérard Lopez sur le nombre 31. C'est lui qui m'a incité à écrire ces programmes.

Alain Barnier
abarnier@wanadoo.fr

Cet article est sous licence Creative Commons Attribution 4.0 International. https://creativecommons.org/licenses/by/4.0/deed.fr

Renseignements pratiques

Ce logiciel peut être utilisé sur tout ordinateur 64 bits sous Windows. Il est gratuit et vous pouvez vous en servir librement.

Vous pouvez l'utiliser en projetant son écran de sortie avec un vidéoprojecteur. Ou alors le faire utiliser par les élèves, seuls ou par deux, derrière leur ordinateur en salle d'informatique. Ils peuvent aussi l'avoir aussi, chez eux, sur leur propre PC.

Il est téléchargeable à partir du lien suivant :

http://alainb-sites.fr/N-premiers/N-premiers-A.exe

La première fois que vous le lancerez (passez toujours outre les recommandations de prudence de Windows), il s'ouvrira dans une petite fenêtre avec, une dimension, des couleurs et une police qui ne vous conviendront peut-être pas. En cliquant droit dans la barre du haut de cette fenêtre, vous aurez accès à ses propriétés et pourrez les modifier à votre aise. Ces modifications resteront enregistrées pour les utilisations suivantes.

Les entrées sont sécurisées, et une faute de frappe ou une entrée incompatible ne plante pas le logiciel.

Il a été testé de nombreuses fois et ne semble pas avoir de bugs.

L'interface du logiciel est simple et toutes les commandes (en nombre limité) sont expliquées ou rappelées en cours d'utilisation.