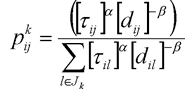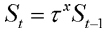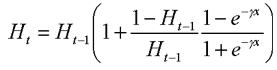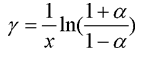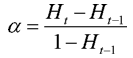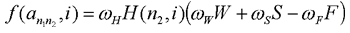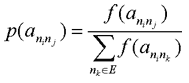|
APPLICATION DE Yann Semet, Pierre Collet PRÉSENTATION DU PROJET DE RECHERCHE EPPAF Pierre Collet, Responsable scientifique du projet EPPAF, Paraschool est le leader français actuel en matière de soutien scolaire à distance, avec environ 50 000 élèves utilisant le logiciel Paraschool, 45 000 dans un cadre scolaire primaire ou secondaire, et environ 5 000 dans un cadre familial par abonnement et connexion internet. Voici presque deux ans, Raphaël Biojout, dirigeant de la société, nous a contacté par mail en ces termes : « Nous souhaitons travailler à un système intelligent qui guiderait plus les élèves dans leur apprentissage et nous aiderait dans la conception et la mise en place de parcours pédagogiques intelligents. » Après avoir passé en revue la plupart des méthodologies d'intelligence artificielle et d'optimisation, il nous est apparu que la technique d'Optimisation par Colonie de Fourmis, apparue à la fin des années 1980 semblait particulièrement bien adaptée au cahier des charges pour au moins deux raisons :
Il est donc possible d'envisager d'associer bijectivement une fourmi à un élève avec l'espoir que (si nous avons suffisamment bien compris les mécanismes qui régissent les fourmis, termites, abeilles et autres insectes sociaux, pour les reproduire artificiellement) puissent apparaître dans le logiciel Paraschool des comportements intelligents et des phénomènes d'auto-organisation du type de ceux observés en franchissant un niveau d'abstraction, comme par exemple :
et tout ceci, sans aucun doute à l'insu des insectes qui en sont à l'origine. Ainsi, grâce au fantastique réservoir d'utilisateurs de Paraschool (et à l'ouverture d'esprit de ses dirigeants), nous allons pouvoir essayer de créer de toutes pièces une « homillière » dans l'environnement informatique virtuel du logiciel Paraschool, ayant pour but collectif de produire un système qui s'adapte dynamiquement aux besoin de chaque élève grâce à l'analyse de ses propres résultats et grâce à l'expérience des erreurs et réussites des autres élèves qui l'auront précédé. Autrement dit, nous espérons que le comportement collectif des élèves permettra de faire apparaître des chemins d'apprentissage menant au succès. En réfléchissant un peu, d'autres « homillières » existent déjà dans ce bas monde. En fait, toutes les structures stables humaines que nous connaissons en sont les produits. Par exemple, l'instinct grégaire et social de l'être humain a abouti à la construction des structures politiques dont on se rend compte qu'elles existent partout de par le monde : ce sont les démocraties, les monarchies mais aussi les dictatures, avec chacune leurs règles, lois et constitutions, leurs organigrammes, leurs organisations bureaucratiques spécifiques... et tout ceci plus ou moins à l'insu de l'individu moyen qui est à leur origine. Il en va de même avec la bourse, où le comportement massif et synchronisé de millions d'actionnaires crée des bulles, des krachs et autres méta-comportements issus d'un comportement collectif. Pour en finir avec les exemples spontanés, Internet est une autre « homillière » dont les caractéristiques techniques (fonctionnalités et limitations) sont probablement responsables de l'émergence de structures et de comportements restant invisibles à notre échelle. Dans le cas de l'« homillière » Paraschool, ce qui est nouveau est que des êtres humains en sont les instigateurs conscients, qui vont essayer d'en canaliser les comportements émergents dans le but d'obtenir « un système intelligent qui guiderait plus les élèves dans leur apprentissage et aiderait dans la conception et la mise en place de parcours pédagogiques intelligents ». Ce projet de recherche doit être mené sans précipitation et sans prendre le moindre risque, car (et c'est encore un cas particulier dans le monde de la recherche) le droit à l'erreur n'existe pas sous peine d'obérer les acquis économiques de la société Paraschool. Dans ce cadre bien particulier, une étude préliminaire a été menée par Benoît Leblanc, dans le cadre d'un stage post-doctoral pour défricher le terrain et s'assurer de la faisabilité du projet, conjointement avec Yannick Jamont, ingénieur de la société Paraschool et Frédéric Marie-Jeanne, responsable de l'équipe pédagogique. Cette étude s'est poursuivie par le stage de fin d'études d'ingénieur de l'Université de Technologie de Compiègne de Yann Semet, qui a donné lieu à deux publications internationales, disponibles par téléchargement à partir de la bibliographie de l'article ci-dessous, qui n'est rien d'autre que le rapport du stage de Yann. Grâce à ce travail, les premiers résultats sont là et sont suffisamment encourageants pour que la société Paraschool souhaite continuer cette collaboration avec le monde de la recherche en finançant la thèse CIFRE de Grégory Valigiani. Les galops d'essais ayant été effectués, les choses sérieuses vont pouvoir commencer avec cette thèse qui débutera le premier octobre prochain... Pierre Collet Yann Semet Résumé Ce rapport décrit le travail effectué dans le cadre d'un stage de fin d'études d'ingénieur à l'UTC. Le travail a été effectué au sein du projet « Fractales », une équipe de recherche de l'INRIA Rocquencourt. L'étude a été réalisée pour le compte de la société Paraschool, gérante d'un site de soutien scolaire en ligne (www.paraschool.com) qui souhaitait rendre son contenu pédagogique plus dynamique, intelligent et attractif. Une technique, inspirée de l'Optimisation par Colonies de Fourmis (ACO) ([9] Bonabeau et al., 1999) a été développée et mise en application. Pour se placer dans le cadre d'un problème d'optimisation, le site Paraschool est modélisé par un graphe où les noeuds représentent les éléments pédagogiques (leçons ou exercices) et les arcs des liens de navigation entre ces éléments. Les étudiants sont représentés par des agents virtuels (des fourmis) qui empruntent ces liens. Chacun des arcs porte par ailleurs une valeur qui décrit son importance pédagogique relativement aux arcs voisins. Le système mis en place, en s'appuyant sur la notion de « stigmergie » (communication indirecte entre agents par le biais de l'environnement) modifie automatiquement cette valeur, qui décrit la structure pédagogique du site, pour que les incohérences disparaissent et pour que les spécificités individuelles et collectives des élèves soient prises en compte. Ce travail tend à soutenir l'idée que les systèmes multi-agents biomimétiques, souvent inspirés des colonies d'insectes sociaux, ont des propriétés cognitives intéressantes d'auto-organisation ou de robustesse au changement, qui les suggèrent comme un outil précieux pour la modélisation ou le soutien de systèmes de cognition collective réelle, une problématique « clé » pour la technologie des Systèmes d'Information I - Introduction : environnement, contexte, déroulement, résultats. Ce travail a été effectué dans le cadre d'une collaboration de transfert technologique entre l'équipe Fractales de l'INRIA Rocquencourt et la société Paraschool. L'Institut National de recherche en Informatique et en Automatique, créé en 1967 à Rocquencourt est un établissement public à caractère scientifique et technologique (EPST) placé sous la double tutelle du ministère de la recherche et du ministère de l'économie, des finances et de l'industrie. Près de 3 000 personnes, ingénieurs, chercheurs ou techniciens y travaillent, réparties sur cinq campus : Sophia-Antipolis, Grenoble, Nancy, Rennes et Rocqencourt. L'équipe Fractales concentre ses activités de recherche autour de deux pôles situés à la frontière des mathématiques appliquées, de l'optimisation et de l'intelligence artificielle : la modélisation fractale de phénomènes complexes et l'algorithmique évolutionnaire. Ces deux pôles bien différents sont unis par le fait qu'ils proposent des approches originales et réfléchies à l'ingénierie et à la compréhension de phénomènes dont la complexité invalide les outils analytiques traditionnels. L'équipe s'articule autour de 3 chercheurs permanents et comporte une petite dizaine de doctorants, autant de collaborateurs extérieurs occasionnels ainsi qu'un nombre variable de stagiaires à court terme. La société Paraschool, créée en 2000, propose une collection d'outils de soutien scolaire en ligne et s'appuie sur une équipe de professeurs qui renseigne en temps réel un contenu qui se veut soigneusement adapté aux besoins des clients . Cette petite entreprise s'appuie également sur une équipe permanente d'une dizaine de personnes, ingénieurs, commerciaux ou graphistes, et occupe aujourd'hui en France une position dominante dans le domaine naissant du « E-Learning ». La collaboration entre Fractales et Paraschool a commencé sous la forme d'un stage post-doctoral de deux mois qui aura servi à jeter les bases du modèle et de l'algorithme utilisé ici. Le stage UTC/TN10 dont il est question ici vient ensuite pour procéder à l'implémentation et à la formalisation du projet en termes scientifiques. Le premier mois est consacré à l'assimilation du problème et à celle de l'architecture web du site Paraschool avec son serveur SQL et choix technologiques d'architecture objet sécurisée basée sur les EJB de Java. Le mois suivant est consacré au codage d'un embryon du système ACO avec un effort particulier pour veiller à ce qu'il soit auto-suffisant et bien intégré à l'architecture Paraschool. Vient ensuite, pendant les deux mois suivants, le temps des expériences de calibrage et des tests de comportements. C'est également à ce moment que le problème est défini en termes scientifiques, comme un problème d'optimisation, et que cette définition, accompagnée des premiers résultats numériques est soumise pour publication à deux conférences internationales. Le mois suivant voit la fin de l'implémentation des raffinements algorithmiques. Le stage s'achève sur un mois partagé entre la finalisation des deux papiers acceptés et la mise en oeuvre du système en conditions réelles. Ce stage s'achève sur les éléments concrets suivants :
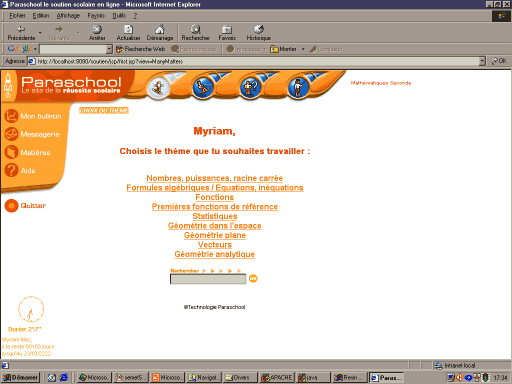
II - Cahier des charges 1. Le site Paraschool Le site Paraschool est un site de soutien scolaire qui propose des compléments pédagogiques, des fiches de cours et des exercices. L'essentiel du contenu concerne les élèves de lycées (seconde, première, terminale) et se concentre sur les mathématiques, la physique et le français. Chaque élève accède au site à l'aide d'un mot de passe et se voit proposer un contenu qui correspond au prix de l'abonnement qu'il paye (une ou plusieurs matières, possibilités d'assistance directe, etc.). Ses résultats sont enregistrés et quelques courbes assorties de commentaires pédagogiques lui permettent de suivre sa propre progression. Passé le choix de la matière à travailler (mathématiques par exemple), l'élève se voit proposer la liste des chapitres qui correspondent à son niveau. La figure 1 donne l'exemple des chapitres de mathématiques d'une seconde générale et donne une idée générale de l'allure de l'interface du site Paraschool.
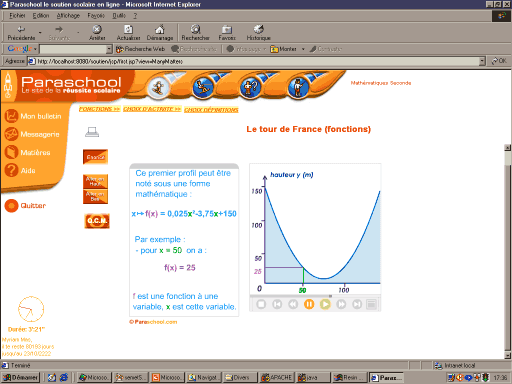
L'élève choisit ensuite une type de travail (définitions, savoir faire, exercice, etc.) puis un point de cours précis (par exemple « définitions » puis « les nombres entiers »). La figure 2 donne en exemple une leçon agréablement illustrée qui porte sur la lecture de représentation graphiques de fonctions mathématiques.
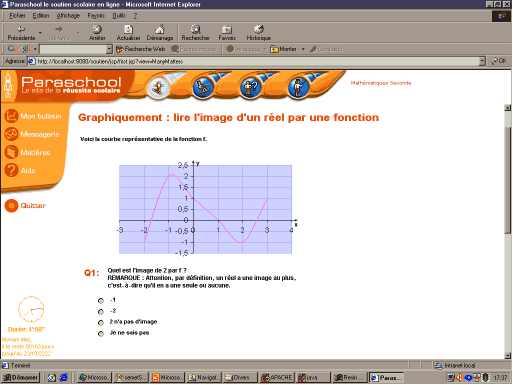
Chaque leçon est suivie d'un exercice interactif, la plupart du temps sous forme de questionnaire à choix multiples comme l'illustre la figure 3 :
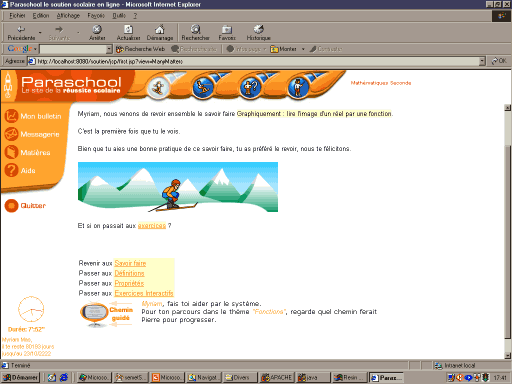
Le résultat est analysé et commenté puis l'élève a la possibilité de cliquer pour retourner à la liste des chapitres ou à celle des types de travaux. C'est ce que montre la figure 4.
L'étudiant peut également, c'est une fonctionnalité nouvelle, se laisser guider interactivement le long d'un chemin (une suite de points de cours) prédéfini par l'équipe pédagogique. Cette opportunité se présente sous la forme d'une petite télévision qui offre un choix à l'élève (voir la figure 5). Cette possibilité était implémentée de façon linéaire et déterministe. C'est ici qu'intervient le système mis en place : la colonie de fourmi aura la charge de proposer une suite intelligente à l'exercice qui vient d'être effectué.
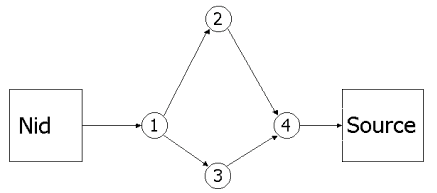
2. Desiderata, objectifs Paraschool cherchait une technique pour rendre son site plus attrayant et plus efficace du point de vue pédagogique. Une intelligence artificielle devait intervenir pour que le site devienne dynamique et sache présenter un contenu adapté à chacun en fonction de ses particularités et de ce que l'expérience collective a montré. Si les réseaux neuronaux et les algorithmes génétiques ont d'abord été évoqué, les algorithmes inspirés des colonies de fourmis, une technique cousine, se sont rapidement imposés comme étant plus simples à écrire, vu leur ressemblance naturelle à la structure du problème à résoudre (population d'agents, optimisation combinatoire, intelligence collective, etc.). L'objectif du système est double. Tous d'abord, il s'agit que la présentation successive des points de cours à valider soit dynamique en s'adaptant automatiquement aux contraintes pédagogiques et aux particularités des individus ainsi qu'en tirant les leçons des événements passés. Ensuite, le système doit servir à mettre en lumière toute cette information, il doit constituer un outil d'audit du contenu pédagogique qui permet aux professeurs de mieux comprendre où et pourquoi les élèves échouent ou réussissent. III - L'optimisation par Colonies de fourmis 1. Contexte et applications L'optimisation par colonies de fourmis est une technique d'optimisation biomimétique inspiré par un travail de biologiste ([3] Deuneubourg et al., 1983) repris par des informaticiens ([4] Moyon et Manderrick, 1988) et largement exploité et développé par Marco Dorigo dans les années 90 ([5] Corlorni et al., 1991 ;[6] Dorigo, 1992). L'idée consiste à imiter le comportement des fourmis réelles qui collaborent, par exemple pour la recherche de sources de nourriture en mélangeant comportement d'exploration aléatoire et suivi des traces chimiques laissées par leur consoeurs. Ces traces chimiques, les « phéromones », sont utilisées par les fourmis pour communiquer entre elles de manière indirecte, par le biais de l'environnement, une technique générale connue par les entomologistes sous le nom de stigmergie. C'est cette forme de communication ainsi que l'idée de faire coopérer une foule d'agents simples et localisés qui forme la base de l'heuristique développée par Dorigo. D'abord appliquée aux problème du voyageur de commerce (voir ci-dessous), l'optimisation par colonies de fourmis a rapidement prouvé son efficacité dans le cadre de l'optimisation combinatoire en général est s'est montré particulièrement profitable pour le problème du routage des paquets d'information dans les grands réseaux d'interconnexion. L'optimisation par colonies de fourmis forme aujourd'hui, avec sa soeur jumelle l'optimisation par essaims particulaires ([11] Kennedy et Russel, 2001), un champ de recherche à part entière, l'intelligence en essaim ou « Swarm Intelligence » ([10] Bonabeau et al., 2000 ; [11] Kennedy et Russel, 2001), voire, à mesure que son champ d'application dépasse les problèmes combinatoires pour s'attaquer aux problèmes multi-objectifs ou aux problèmes de design cognitif comme c'est le cas ici, une nouvelle façon de concevoir l'intelligence artificielle à base d'agents. 2. Un cas emblématique Pour mieux comprendre la façon dont fonctionnent les colonies de fourmis, reprenons l'exemple traditionnellement donné pour illustrer leur capacité à trouver des chemins optimaux. La figure 6 illustre une situation où il y a un nid, où les fourmis vivent, et une source de nourriture, que les fourmis doivent trouver et dont elles doivent ramener les provisions vers le nid.
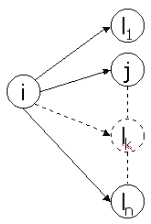
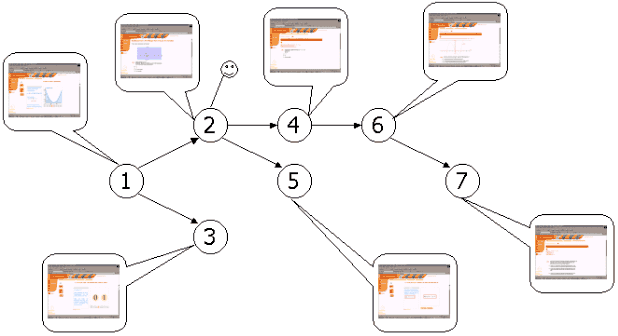
Il existe deux chemins possibles pour atteindre la source : un long, un court. Les fourmis explorent aléatoirement les deux. Lorsqu'elles trouvent la source, elles se chargent de nourriture, et retournent au nid par où elles sont venues en libérant des phéromones tout au long de leur chemin. Le chemin le plus court étant aussi le plus rapide, sa concentration en phéromones augmentera plus vite et les fourmis, qui suivent les traces chimiques, seront très vite, par un phénomène de renforcement, encouragées à suivre le chemin le plus court. Le chemin du nid à la source a été optimisé. Cette façon de procéder est déjà efficace en soi mais il manque deux phénomènes essentiels pour qu'elle soit tout à fait complète. Cet exemple illustre bien la façon dont les colonies de fourmis s'adaptent de manière optimale à leur environnement en pondérant information locale, information stigmergique et comportement aléatoires. Cet exemple particulier sera repris comme test canonique pour les premières expériences de calibrage du système Paraschool (voir section Résultats). 3. Le principe par l'exemple : application au problème du voyageur de commerce Pour illustrer la manière dont on peut transformer l'observation de colonies de fourmis réelles en algorithme d'optimisation, on reprend ici l'exemple traditionnel de la résolution du problème du voyageur de commerce avec un algorithme à base de fourmis artificielles ([7] Stützle et Dorigo, 1999 ; [8] Stützle et Hoos, 1997). Le problème du voyageur de commerce, pour le rappeler brièvement consiste à trouver un chemin Hamiltonien dans un graphe complètement connecté. En termes plus imagés, il s'agit pour un voyageur de commerce de trouver le chemin le plus court pour visiter une et une seule fois chacune des n villes dans lesquelles il doit se rendre. Il s'agit sans doute du problème d'optimisation combinatoire NP-complet le plus utilisé comme test pour les nouvelles méthodes d'optimisation. Les fourmis vont travailler en parallèle à essayer diverses solutions à ce problème jusqu'à en trouver une acceptable. On procède de la manière suivante : Chacune des fourmis de la colonie est placée au hasard sur un des noeuds du graphe. Chacune commence alors sa « tournée » : elle se rend de noeud en noeud sans jamais en visiter un qu'elle a déjà vu et jusqu'à ce qu'elle les ait tous visités. Le choix du passage d'un noeud i à un noeud j (voir figure 7) se fait aléatoirement en fonction d'une probabilité donnée par l'équation 1. d y décrit la distance entre les noeuds i et j (information heuristique locale, la fourmi a tendance à aller au plus près) et t la quantité de phéromones déposées sur l'arc correspondant. a et b servent à régler l'importance relative que l'on donne à ces deux facteurs.
Après n itérations, lorsque toutes les fourmis ont construit un chemin complet, chacune d'elles calcule la longueur totale parcourue (somme des distances d'une ville à l'autre) et libère des phéromones tout au long du chemin en quantité inversement proportionnelle à la longueur : plus le chemin est court, plus il sera chargé en phéromones. Le procédé est alors recommencé jusqu'à ce l'on obtienne une solution optimale ou jugée acceptable. Régulièrement par ailleurs, les quantités de phéromones portées par les arcs sont multipliées par un facteur d'évaporation typiquement proche de 0.99. Cette façon d'explorer l'espace de recherche a le mérite d'être efficace et d'offrir un compromis entre l'exploitation de l'information apportée par la collectivité (les phéromones préalablement déposées là où les fourmis ont intérêt à passer), l'utilisation des heuristiques locales (allons au plus près !) et l'exploration aléatoire. Les méthodes ACO (Ant Colony Optimisation) , hybridées avec des heuristiques de recherche locale bien choisies (type Lin-Kerningan ou 3-opt) sont parmi les meilleures pour les problèmes TSP (Travelling Salesman Problem) de grandes tailles ([7] Stützle et Dorigo, 1999 ; [8] Stützle et Hoos, 1997). C'est directement de cet algorithme que l'on s'est inspiré pour écrire celui qui va tenter d'optimiser le cheminement des élèves dans le site Paraschool. La section suivante explique comment l'analogie, et donc le modèle, ont été construits. IV - L'Algorithme 1. Modélisation : W ou la structure pédagogique
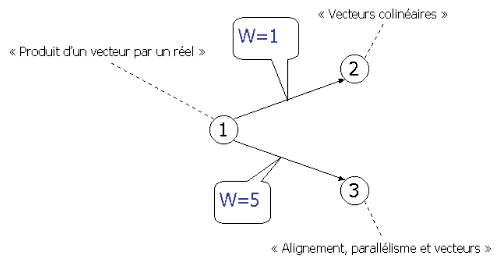
Le site web de Paraschool est modélisé par un graphe où chaque noeud représente un élément pédagogique (exercice, leçon, voir figure 8) et chaque arc une navigation possible entre deux éléments (lien hypertexte). Chacun de ces arcs porte une valeur réelle nommée W qui représente sa « pertinence » pédagogique. Cette valeur est relative et place l'arc par rapport à ses voisins, c'est-à-dire par rapport aux arcs qui sortent du même noeud que lui. Comme la figure 9 l'illustre, selon l'équipe pédagogique, après avoir vu « Produit d'un vecteur par un réel », il est cinq fois plus adéquat d'aller voir « Alignement, parallélisme et vecteurs » que d'aller voir « Vecteurs colinéaires ». L'élève n'est pas obligé de suivre la suggestion faite par les fourmis : s'il le souhaite, il peut se diriger vers un noeud non suggéré. Si l'arc alors emprunté n'existe pas, il est créé avec W portant la valeur 1 qui est la valeur par défaut. Lors de son utilisation pour les calculs de fitness (voir plus bas), cette valeur W est réduite par rapport à ses voisins ; autrement dit, le vecteur portant les poids pédagogique sortant du noeud considéré est normalisé.
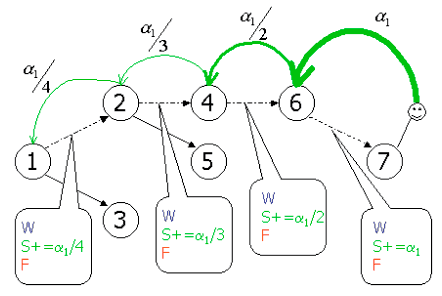
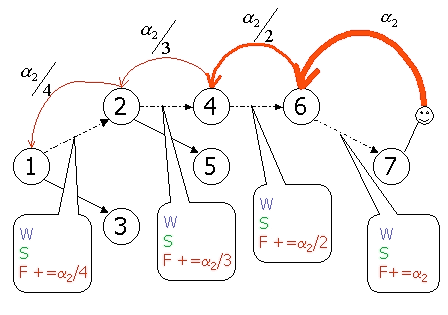
2. Fourmis et phéromones : S et F Chaque élève qui parcourt le graphe est représenté par une « fourmi », un micro-agent, qui navigue sur le graphe sous-jacent. À l'issue de chaque exercice, ou de chaque leçon suivie d'un questionnaire, la fourmi libère des phéromones. Si l'exercice est validé avec succès, ce seront des phéromones de succès (S), sinon ce seront des phéromones d'échec (F pour Failure). Chaque arc portera donc, en plus de W, deux valeurs S et F. Rétro-propagation et portée pédagogique spatiale Les phéromones, qu'il s'agisse de S ou de F ne sont pas simplement libérées sur l'arc qui a mené la fourmi au noeud/exercice courant mais sur les n derniers arcs que la fourmi a suivi. Ceci est fait pour refléter le fait pédagogique que le succès (ou l'échec) à un endroit donné est conditionné par ce qui a été vu avant par l'élève. Bien évidemment, cette influence diminue avec le temps et l'espace : plus le noeud est éloigné dans l'histoire de la fourmi, moins il a d'importance. Pour que cela soit pris en compte, la quantité de phéromone déposée diminue à mesure que la rétro-propagation avance. Numériquement, n est fixée à 4 et l'amplitude diminue en 1/k partant d'une valeur a prédéfinie, paramètre du système. Les figures 10 et 11 illustrent la rétro-propagation : après avoir réussi (ou échoué) au noeud 7, une quantité a de phéromones est déposée sur l'arc
Figure 10 : Rétro-propagation des phéromones de succès.
Figure 11 : Rétro-propagation des phéromones d'échec. Évaporation Le fait que les phéromones naturelles s'évaporent avec le temps est extrêmement important car cela permet à la colonie de fourmis de se fier à des informations constamment mises à jour. Dans notre système artificiel, il est important d'implémenter une forme d'évaporation pour éviter que le système ne reste « coincé » dans un optimum local ainsi que pour ouvrir la porte aux caractéristiques attendues d'adaptativité dynamique.
L'équation 2 donne la forme de l'évaporation pour les phéromones de succès S (l'équation est identique pour F) : t, le taux d'évaporation, est un paramètre clé du système dont on verra l'une des conséquences dans les tests de simulation décrits plus bas. La période d'évaporation, x qui dit à quels intervalles l'évaporation est calculée est une constante pédagogique. Typiquement, t=0.999 et x=1 jour. 3. Un premier facteur individuel : H Les valeurs W, S et F évoquées jusqu'ici sont des facteurs dits collectifs, ils concernent l'ensemble des élèves qui vont se servir de l'information qu'elles contiennent pour construire leur cheminement. W est exogène, elle est apportée par l'équipe pédagogique à la collectivité d'étudiants/fourmis. S et F sont endogènes, elles sont créées par les individus pour le service de la collectivité : intelligence immergée, culture émergente. Le système doit également être en mesure de prendre en compte des facteurs individuels, propres à chaque étudiant, pour pouvoir réaliser le compromis que l'on cherche entre l'individu, la collectivité et l'environnement. Les facteurs individuels que l'on peut prendre en compte sont nombreux (préférences, excellence, agenda de travail, etc.), celui qui est implémenté ici en est un exemple : il s'agit du facteur historique, H, qui porte l'information sur les noeuds précédemment visités dans l'histoire de l'étudiant. Cette valeur H sera utilisée dans le calcul de l'« adéquation » de la valeur portée par les arcs (que nous appellerons plus bas « fitness ») comme un facteur multiplicatif de valeur par défaut 1. Puisqu'il s'agit d'un facteur individuel, il existe une valeur H par étudiant et par noeud (H est une application de N×I dans R où I est l'ensemble des individus/étudiants/fourmis). Lorsqu'un noeud est visité par un étudiant, la valeur H correspondante est multipliée par h1 s'il s'agit d'un succès, h2 s'il s'agit d'un échec. Typiquement, h1=0.5 et h2=0.75. Le rôle de H est de diminuer la probabilité que le noeud déjà visité soit à nouveau proposé. Bien sûr, si le noeud a été le siège d'un échec (cas h2) il sera plus vite reproposé que si il y a eu succès (cas h1), c'est ce qui explique que h2>h1. À mesure que le temps passe, bien sûr, les élèves oublient ce qu'ils ont vu. C'est pour cela que H tend à revenir naturellement vers 1. Cette « anti-évaporation » est décrite par l'équation 3.
g est une constante de temps qui règle la vitesse du phénomène. Il faut qu'elle soit réglée pour correspondre à la volatilité de la mémoire des étudiants. Il s'agit donc d'une constante pédagogique qui doit faire l'objet d'un dialogue avec les professeurs. Les équations 4 et 5 permettent un calibrage facile de g. On procède en effet de la manière suivante : il faut d'abord définir ce qu'« oublier un exercice » signifie, par exemple : si sa valeur H passe de 0.5 à 0.9. Ceci donne a » 2.2. L'équipe pédagogique n'a plus qu'à dire le temps qu'il faut pour « oublier un exercice ». Une semaine par exemple (604 800 secondes) donne
4. Une mesure de fitness Tous les facteurs décrits précédemment (W, S, F et H) sont unifiés par une fonction dite de « fitness », par analogie avec la littérature des algorithmes génétiques. Cette fonction, donnée par l'équation 6, mesure l'excellence d'un arc donné, sa « désirabilité », et va conditionner, par le biais d'une procédure de sélection, la probabilité que l'arc considéré soit suggéré aux étudiants.
On remarque qu'un arc est désirable lorsque :
On remarque également que l'importance relative des différents facteurs est configurable par le biais des wi. 5. Procédures de sélection Lorsqu'un étudiant valide un noeud, il convient de choisir, parmi les arcs qui sortent de ce noeud, celui qui est le plus adéquat à emprunter, c'est le rôle de la procédure de sélection. C'est ici que sont utilisées les mesures de fitness. Une procédure de sélection va choisir un arc aléatoirement mais d'autant plus probablement que la fitness de l'arc est élevé. On verra ainsi les arcs « efficaces » devenir prédominants mais pas de manière exclusive, il y aura de la place pour le hasard et l'exploration. Cette part de hasard est une caractéristique cruciale de la procédure de sélection, on parle de pression sélective ou s. Plus s est grande, plus le tirage se laisse guider par la fonction de fitness et plus les arcs forts auront tendance à dominer les arcs faibles. Il existe différentes façon d'écrire l'algorithme de sélection et par conséquent de paramétrer s. Cinq méthodes classiques ont été implémentées :
Si beaucoup de travaux ont été conduits pour étudier les procédures de sélection dans le cadre des algorithmes génétiques, peu ou pas d'études portent sur leur impact dans le cadre des algorithmes à colonie de fourmis. C'est donc un problème ouvert. Si la plupart des arguments restent entiers, il est important de comprendre que le contexte est différent. Trois intérêts antagonistes doivent guider le choix de la procédure de sélection :
Il faut donc choisir une procédure et ses paramètres de manière compétente en cherchant à obtenir un compromis raisonnable entre ces trois intérêts. La plupart des expériences ont été conduites avec un tournoi stochastique. V - Tests et application Au delà des tests de « déboguage », et avant la mise en service effective, la mise à l'épreuve du système décrit précédemment se déroule en deux étapes. Des simulations sont faites d'abord pour obtenir un calibrage global des paramètres numériques et vérifier le comportement du système dans quelques cas particuliers mais importants. Le système est ensuite greffé à l'architecture web du site Paraschool pour un premier contact avec le « monde réel ». 1) Simulations Postulats Les expériences de simulation sont conduites sur quatre graphes types, dans l'ordre suivant :
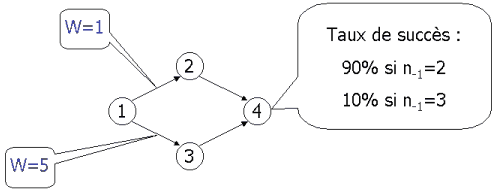
Pour simuler les succès et échecs des élèves, chacun des noeuds de ces graphes de test se voit attribuer un niveau de difficulté, tiré aléatoirement et représenté par un nombre réel compris entre 0 et 1. De même, les étudiants sont simulés par des entités virtuelles qui parcourent le graphe en suivant le guidage du système. Chacune de ces « fourmis » se voit attribuer un niveau d'« excellence » compris lui aussi entre 0 et 1. La validation d'un noeud/exercice est alors résolue en comparant le niveau de difficulté du noeud et l'excellence de la fourmi. Par exemple, si la fourmi n° 932, portant une excellence de 0.86 arrive au noeud n° 14 de difficulté 0.74, la fourmi réussit le noeud et libère des phéromones de succès en conséquence. b) Un cas emblématique Une des caractéristiques attendues de l'heuristique choisie, celle des colonies d'insectes sociaux, est la capacité à détecter automatiquement les incohérences et à les éliminer graduellement. Il s'agit d'être autonome et intelligent vis-à-vis d'un environnement piégé et de choix passés rendus obsolètes. L'exemple choisi ici pour illustrer cette capacité et vérifier que notre système la possède bien est inspiré de l'exemple traditionnellement pris chez les fourmis et repris plus haut ici (cf. figure 6). La situation est transposée en termes pédagogiques et illustrée par la figure 12. Partant de l'exercice 1 et pour aller à l'exercice 4, les fourmis/étudiants ont deux possibilités : passer par l'exercice 2 ou par l'exercice 3. L'équipe pédagogique à cru bon d'encourager le passage par l'exercice 3 en lui attribuant un poids W bien supérieur (5 contre 1). Les élèves ont donc une probabilité 5 fois supérieure de se voir proposer l'arc
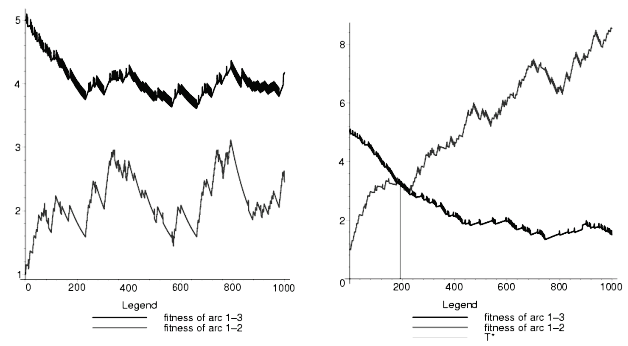
L'expérience montre que le comportement souhaité (une inversion stable dans le temps des mesures de fitness des deux arcs) n'apparaît pas systématiquement et qu'il est important de se situer dans une zone de paramétrage adéquate. Les figures 13 et 14 illustrent le comportement du système en fonction d'un paramètre clé, le taux d'évaporation. Si ce dernier est trop élevé, le dépôt de phéromones n'a pas le temps de faire effet et les mesures de fitness ne cessent d'osciller sans jamais ni s'inverser ni se stabiliser. Lorsque l'on réduit t , passant de 0.99 à 0.999, soit à une évaporation plus lente, on observe, comme illustré par la figure 14, le comportement attendu : les mesures des deux arcs s'inversent et cette inversion perdure. Les élèves sont donc encouragés à faire l'exercice qui les prépare le mieux à la suite. Cette première expérience a deux intérêts : elle démontre empiriquement l'existence d'une caractéristique attendue de l'algorithme mis en place et permet de se faire une idée de la position des zones de l'espace de paramètres qui permettent l'existence de cette caractéristique.
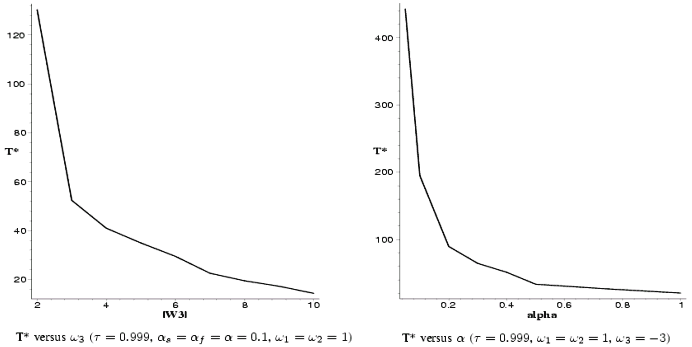
Une deuxième expérience de calibrage est conduite alors qu'on se place dans les zones adéquates susmentionnées. S'il est important de montrer cette possibilité d'inversion des mesures incohérentes, il est plus intéressant encore d'avoir un minimum de contrôle sur les caractéristiques de cette inversion, en particulier sur sa vitesse. Cette vélocité caractérise la promptitude du système à réagir aux informations apportées par l'interaction entre les élèves et l'environnement, elle caractérise son inertie. On choisit de caractériser cette inertie par une valeur que l'on nomme t* et qui représente l'itération à laquelle l'inversion des deux mesures de fitness s'est produite. Le nom de cette valeur est choisie par analogie avec le takeover time de la littérature des algorithmes génétiques et qui mesure le temps qu'il faut au meilleur individu pour remplir la population sous l'effet du seul opérateur de sélection. Il s'agit d'un moyen de mesurer la pression sélective, autrement dit la réactivité de la population génétique à la distribution de la fitness parmi ses membres, dans des conditions réduites au plus simple possible pour faciliter la compréhension d'un phénomène précis mais fondamental pour le succès de l'algorithme. Similairement ici, on se restreint à des conditions expérimentales très réductrices pour se concentrer sur un phénomène clé que l'on tente de caractériser simplement pour pouvoir le contrôler. Les figures 15 et 16 donnent la valeur de t* (on se place implicitement dans des conditions où t* existe) en fonction de deux paramètres différents (wF et a2). Ce genres de courbes permet de choisir une vélocité que l'on considère comme adéquate et de régler les paramètres du système en conséquence. Cette vélocité est un paramètre très important du système et doit se régler en fonction de constantes de temps basés sur des indicateurs pédagogiques. Un système dynamique trop lent ne pourrait pas réagir aux variations de l'environnement pédagogique et présenterait une adaptativité retardée et non pertinente. Inversement, un système trop rapide pourrait devenir chaotique, trop sensible au bruit et s'avérer tout aussi peu pertinent.
Il est important de souligner que cet exemple n'est qu'emblématique de la façon dont on peut illustrer la puissance du système et le calibrer numériquement pour contrôler son comportement. Il convient donc de s'attacher plus à l'esprit de ces résultats qu'à leur lettre, ceci pour les deux raisons suivantes. Tout d'abord, les valeurs numériques ne sont pas à prendre telles quelles puisque les expériences sont conduites sur un graphe réduit et sorti de son contexte réel et pédagogique. Ensuite, il ne s'agit que d'un exemple dans la mesure où il n'est pas forcément souhaitable que la structuration pédagogique cherche systématiquement à éluder les difficultés. La pédagogie est un art subtil qui passe parfois par une forme de coercition que l'élève peut ressentir comme dénuée de sens mais dont il récoltera les fruits plus tard. Les professeurs peuvent délibérément faire le choix de la pédagogie inversée en forçant les élèves à suivre un chemin particulièrement difficile et semé d'échecs. Il est donc crucial que le dialogue avec l'équipe pédagogique soit placé au premier plan et que les effets d'auto-adaptation soient contrôlés (par exemple en établissant des bornes numériques sur les valeurs de phéromones) pour qu'ils n'empiètent pas sur la stratégie pédagogique des professeurs. L'objectif du système n'est pas de prendre un parti plutôt que l'autre (élèves ou professeurs) mais de trouver un compromis naturel : supprimer les absurdités, détecter les particularités de chacun ou du groupe, mais garder en vue le cap pédagogique fixé. Mise en service silencieux Après les tests de simulation décrits ci-dessus, le système a été intégré à l'architecture du site web de Paraschool. Passée la phase d'intégration, forcément délicate dans le cadre d'une architecture objet distribuée, le système a été mis en application en mode dit silencieux. Cela signifie que le système ne fait qu'observer les pérégrinations des élèves sans qu'encore il leur soit visible. Chaque étudiant est bien suivi par une fourmi qui libère des phéromones mais les arcs, issus des procédures de sélection ne sont pas proposés aux étudiants, qui continuent à utiliser le logiciel Paraschool comme si de rien n'était. Si ce mode d'observation ne permet pas de tirer de conclusions fondées quand à la capacité du système à se comporter intelligemment comme exemplifié dans les tests de simulation en présence d'étudiants réels, il permet déjà de se faire une idée de sa bonne marche en condition réelles et l'on peut d'ores et déjà se faire une idée sur :
Pour ce dernier point, il convient de rappeler l'importance qu'accorde Paraschool au système développé en tant qu'outil d'audit pédagogique. L'outil tel qu'il est, avant même sa mise en application réelle et la mise en oeuvre de ses velléités d'organisation intelligente, apparaît déjà comme satisfaisant de ce point de vue et a pu donner jour à quelques discussions pédagogiques qui n'avaient pas eu lieu auparavant autour, par exemple, de noeuds singuliers, non pas faute d'avoir les informations ad hoc, mais faute d'en avoir une présentation concise et efficace. Un algorithme ACO n'est sans doute pas un outil d'audit pédagogique très raffiné mais il a le mérite d'apporter cet audit gratuitement et de présenter quelques informations avec simplicité en termes directs et localisés. Pour Paraschool , il semblerait que cette information là satisfasse les besoins d'une première démarche de questionnement du contenu. Conclusion Ce mémoire détaille l'application d'une technique d'Intelligence Artificielle de pointe, l'Optimisation par Colonies de Fourmis, à un problème de structuration d'un système d'information en procédant à l'adaptation automatique des voies de navigation hypertexte. Le stage s'achève sur une implémentation complète, une méthode scientifique formalisée et des premiers résultats prometteurs. Pour un élève ingénieur, l'enrichissement est triple. Techniquement d'abord, il aura fallu à la fois concevoir et implémenter un algorithme d'optimisation stochastique puis l'intégrer intelligemment dans une architecture objet distribuée complexe et structurée par des contraintes de rigueur fortes due à une utilisation en temps réel. Il en ressort des méthodes d'écriture algorithmique rigoureuse et des réflexes de programmeur intégré à une équipe de développement orienté objet. Du point de vue scientifique, ensuite, c'est la découverte de la chaîne qui mène de l'investigation en littérature à la défense publique de méthodes de résolution d'un problème nouvellement formalisé. L'efficacité de lecture et de rédaction anglophones ainsi que la découverte des rudiments d'une méthodologie constructive et critique ne sauraient manquer de s'avérer précieuses pour un ingénieur. Finalement, ce sont sans doute les leçons tirées d'un rôle de trait d'union entre interlocuteurs qui formulent un problème en termes différents, parce qu'ils n'ont pas les mêmes intérêts, qui s'avéreront les plus profitables. C'est l'une des missions fondamentales des ingénieurs que de mettre la science au service des entrepreneurs et ce stage apparaît comme un exemple de transfert technologique réussi. Yann SEMET Une suite... Grâce à ce travail, les premiers résultats étant là et suffisamment encourageants, la société Paraschool a souhaité continuer cette collaboration avec le monde de la recherche en finançant la thèse CIFRE de Grégory Valigiani. Il en est ressorti le développement du concept de Hommilière, prolongement naturel, dans ce contexte, de celui de Colonie de Fourmis. Voir l'article Projet ECHO. Étude Comportementale des Hommilières pour l'Optimisation. [1] Semet Y., Jamont Y., Biojout R., Lutton E. et Collet P., 2003. « Artificial Ant Colonies and E-Learning: An Optimisation of Pedagogical Paths », Proceedings of HCII'03 - Human Computer Interaction International. Crète, Grèce. 22-27 juin 2003. [2] Semet Y., Lutton E. et Collet P., 2003. « Ant Colony Optimisation for E-Learning: Observingthe Emergence of Pedagogic Suggestions », IEEE Swarm Intelligence Symposium, Indianapolis, USA, 24-26 avril 2003. [3] Moyson F. et Manderick B., 1988. « The Collective Behaviour of Ants: an Example of Self-Organisation in Massive Parallelism », Proceedings of the AAAI Spring Symposium on Parallel Models of Intelligence. Stanford, California. [4] Deneubourg J.-L., Pasteels J.-M. et Verhaeghe J.-C., 1983. « Probabilistic Behaviour in Ants: a Strategy of Errors ? », Journal of Theoretical Biology, 105. [5] Colorni A., Dorigo M. et Maniezzo V., 1991. « Distributed Optimization by Ant Colonies », Proceedings of the First European Conference on Artificial Life, MIT Press/Bradford Book, Paris. [6] Dorigo M., 1992. Optimization, Learning and Natural Algorithms, PhD thesis, Dipartimento di Electronica, Politecnico di Milano, IT. [7] Stützle T. et Dorigo M., 1999. « ACO Algorithms for the Travelling Salesman Problem », in M Makela, K Miettinen, P Neittaanmaki, J Periaux (Eds), Proceedings of the EUROGEN conference, John Wiley & Sons, ISBN: 0471999024. [8] Stutzle T. et Hoos H., 1997. « The Max-Min ant system and local search for the Travelling Salesman Problem », T. Baeck, Z. Mickalewicz and X. Yao, editors, Proceedings of IEEE-ICEC-EPS'97 International Conference on Evolutionary Computation and Evolutionary Programming, IEEE Press, p. 309-314. [9] Bonabeau E. , Dorigo M., and Theraulaz G., 2000. « Inspiration for optimization from social insect behaviour », Nature, vol. 406, 6 July 2000. [10] Bonabeau E., Dorigo M., et Theraulaz G., 1999. Swarm Intelligence: From Natural to Artificial Systems, Oxford University Press. ISBN 0-19-513159-2. [11] Kennedy J. et Eberhart R. C., 2001. Swarm Intelligence, Morgan Kaufmann Publishers, San Francisco, California. __________________ |