Construire une séquence pédagogique
utilisant un logiciel de simulation de gaz
 

B. Outils pour la construction d'une séquence

B.1. Compléments sur la théorie cinétique et le modèle du gaz parfait

Avec la simulation, nous voulons montrer comment la théorie cinétique des gaz permet de donner une signification physique à la pression et à la température et comment les relations entre les variables qui caractérisent l'état d'un gaz - pression p, volume V, température T et quantité de gaz n - peuvent s'expliquer simplement par le mouvement des molécules. Les molécules sont supposées animées de mouvements incessants, qui constituent l'agitation thermique.

Au niveau macroscopique, la pression en un point d'un fluide p = F/S (en Pa) est introduite par la force, par unité de surface, que le fluide exerce sur une surface élémentaire placée en ce point, suivant la normale. La température absolue T (en Kelvin) est la variable qui décrit l'état thermique d'un gaz. Pression p et température T sont des grandeurs positives.

L'équation d'état du gaz parfait

Les lois historiques qui traduisent le comportement des gaz ont été établies expérimentalement à partir de gaz réels, suffisamment dilués :

· Loi de Boyle et Mariotte (1660)
À température constante, le produit pV de la pression par le volume est constant.

· Loi d'Avogadro (1811)
Des volumes égaux de gaz parfaits, à la même pression et à la même température, contiennent la même quantité de matière (en moles).

· Loi de Gay-Lussac (1802)
À pression constante, le volume occupé par une quantité déterminée de gaz parfait est proportionnel à la température absolue T.

· Loi de Charles (1795)
À volume constant, la pression d'une quantité déterminée de gaz parfait est proportionnelle à la température absolue T.

Rassemblées en une seule loi, la relation entre pression, volume, température et quantité de matière, définit l'équation d'état des gaz parfaits. Elle s'écrit pV = nRT où R est la constante des gaz parfaits R = 8,31 J/K/mol.
Un gaz réel se rapproche d'autant plus d'un gaz parfait qu'il se trouve dans des conditions de température et de pression éloignées des conditions de liquéfaction.

La théorie cinétique des gaz

L'interprétation microscopique de la pression d'un gaz fut proposée pour la première fois par Bernoulli en 1738. La force pressante exercée par un gaz sur une paroi est due au bombardement de cette paroi par les molécules du gaz. On l'évalue à partir de la variation de la quantité de mouvement des molécules après collision avec la paroi, c'est-à-dire la quantité de mouvement cédée à la paroi. Il en est de même pour toute surface fictive à l'intérieur du fluide.
Maxwell (1859) et Boltzmann (1872) ont contribué à la compréhension en termes microscopiques des phénomènes thermodynamiques. La théorie cinétique des gaz a été élaborée par Maxwell, dans le cas du gaz parfait. Elle s'appuie sur le modèle moléculaire de la représentation des gaz, proposé par Avogadro en 1811 et sur des considérations statistiques, le nombre de molécules d'un gaz à notre échelle macroscopique étant considérable, de l'ordre du nombre d'Avogadro N_A = 6,02×10²³.

Le modèle du gaz parfait est défini à partir de trois hypothèses :

• les molécules sont assimilées à des sphères dures de diamètre négligeable devant la distance qui les sépare ; il en résulte qu'un gaz réel dilué se comporte comme un gaz parfait.

• les interactions entre molécules sont localisées dans les collisions, que l'on suppose élastiques. Au cours du choc d'une molécule avec la paroi, il n'y a ni gain ni perte d'énergie, il y a conservation de la quantité de mouvement, selon les lois de la mécanique newtonienne applicables à des sphères dures. On suppose la paroi et le gaz à la même température.

• les positions des molécules et leurs vitesses sont distribuées au hasard selon les trois directions de l'espace : c'est le chaos moléculaire caractéristique de l'équilibre.

Les hypothèses statistiques de Maxwell précisent la loi statistique associée au chaos moléculaire :

• uniformité de la répartition des molécules, en l'absence de champ extérieur,

• isotropie des vitesses,

• indépendance des composantes des vitesses.

En combinant ces deux séries d'hypothèses, mécaniques et statistiques, on peut exprimer simplement la pression cinétique d'un gaz en considérant les collisions avec la paroi. L'encadré 1 résume les principales étapes d'un calcul simplifié de la pression cinétique. On montre que la pression p = F/S (force pressante par unité de surface exercée par le gaz sur la paroi du récipient) est proportionnelle à l'énergie cinétique moyenne des molécules E_C = 1/2 mu² et au nombre de molécules par unité de volume N/V : p = 1/3 Nmu²/V où u est la vitesse quadratique moyenne des molécules.

À partir des lois des gaz parfaits, en considérant N molécules d'un gaz parfait, contenues dans un volume V à la pression p, la température absolue T (en kelvin) est définie par la relation pV = NkT. En comparant les deux expressions précédentes, la température absolue T est proportionnelle à l'énergie cinétique moyenne des molécules : 1/2 mu² = 3/2 kT (encadré 2). En posant pV = RT pour une mole, on calcule R, constante des gaz parfaits.

La simulation « Atelier théorie cinétique des gaz »

La simulation visualise sur le registre symbolique le mouvement aléatoire de molécules de gaz régi par les lois précédentes. La compréhension des conséquences de ce mouvement s'appuie sur un raisonnement par analogie entre deux échelles : on vérifie que les lois connues de la mécanique appliquées aux objets macroscopiques s'appliquent aussi aux objets microscopiques (quelques particules sur l'écran) et se traduisent sur l'image.

La simulation met en scène une « clé didactique », issue de résultat de recherches (Rozier 1988, Méheut 1996) pour aider à interpréter la pression comme due aux effets des chocs sur les parois. En effet la pression cinétique p = 1/3 Nmu²/V apparaît comme produit de deux facteurs p = 1/3 (Nu/V) (mu) dont la signification physique est la suivante :

• le nombre moyen de molécules qui arrivent sur la paroi par unité de surface et de temps, équivalent au nombre de chocs sur la paroi par unité de surface et de temps ou fréquence des chocs par unité de surface. Ce nombre est proportionnel à (Nu/V), où u est la vitesse quadratique moyenne et N/V la densité de molécules. Ce nombre moyen est affiché sur l'écran ;

• la quantité de mouvement échangée avec la paroi lors du choc d'une molécule, un facteur « dynamique » (mu) proportionnel à

  • la vitesse quadratique moyenne de la molécule, à masse donnée,
  • la masse de la molécule, à vitesse quadratique moyenne donnée.
  Cette grandeur est à associer de façon intuitive à l'idée de « violence » du choc ou « force » du choc et donc à construire avec appui sur les situations simulées.

Toute augmentation de la vitesse quadratique moyenne des molécules d'un gaz donné se traduit par deux effets simultanés sur les chocs : les chocs sont à la fois plus fréquents et plus « forts ».

Dans la pratique enseignante courante, la température, liée à « l'agitation » moléculaire, est souvent associée à la seule vitesse des molécules. Lorsque la température est fixée, le logiciel calcule la répartition des vitesses autour de la vitesse quadratique moyenne du type de molécules choisi en respectant la relation entre température T et énergie cinétique moyenne 1/2 mu². Plus précisément, deux gaz parfaits différents en interaction évoluent vers un état d'équilibre statistique caractérisé par l'égalité des énergies cinétiques.

On observe sur l'image que :

• à T donnée, toutes les molécules de même masse n'ont pas la même vitesse, (image de la variabilité de la vitesse) ;

• les molécules s'agitent d'autant plus que la température T augmente : pour un type donné de molécules (à masse donnée), la vitesse quadratique moyenne augmente ;

• à T donnée, les vitesses quadratiques des molécules de gaz différents étant dans le rapport inverse des racines carrées de leurs masses molaires u₁/u₂ = (M₂/M₁)^1/2, les particules plus lourdes ont des vitesses plus faibles. à T donnée, « l'agitation » moyenne dépend aussi de la masse d'une particule.

Encadré 1. Pression cinétique et effets des chocs sur les parois : étapes d'un calcul simplifié. (D'après Ogborn et al. 2000)

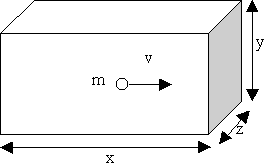
Hypothèses statistiques et lois de la mécanique newtonienne Une molécule dans une boîte v perpendiculaire à la paroi   Chocs élastiques : conservation de la quantité de mouvement - lors du choc de la molécule sur la paroi       quantité de mouvement avant = + mv       quantité de mouvement après = - mv - la variation de la quantité de mouvement :       de la molécule DP = -2mv       de la paroi DP = +2mv temps de parcours entre deux chocs Dt = 2x/v nombre de chocs par seconde = v/2x - d'après la relation fondamentale de la dynamique la force exercée par la paroi sur la molécule vaut : f = (nombre de chocs/s) × (variation de la quantité de mouvement) f = (v/2x) × (-2mv) - d'après la loi des interactions réciproques : force exercée par la molécule sur la paroi = mv2/x pression p = force par unité de surface (S = y.z) p = mv2/x y z pression p = mv2/V N molécules se déplacent de la même façon 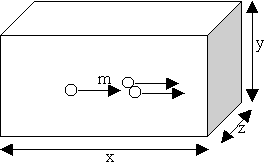N fois le nombre de chocs par seconde pression p = Nmv2/V   N molécules se déplacent au hasard avec isotropie des vitesses 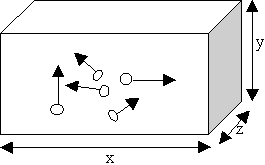1/3 des molécules dans chaque direction en moyenne 1/3 des chocs par seconde pression p = 1/3 Nmv2/V   N molécules se déplacent avec des vitesses distribuées au hasard selon la loi de Maxwell-Boltzmann prendre la moyenne sur v2, u vitesse quadratique moyenne p = 1/3 Nmu2/V

 
Encadré 2. Température et énergie cinétique moyenne des molécules

Phénomènes à interpréter à l'aide du modèle cinétique des gaz

- Propriétés thermoélastiques des gaz
Reprendre chacune des lois macroscopiques et les interpréter avec le modèle cinétique.
Prévoir et interpréter le comportement de gaz dans des situations classiques : gonfler un pneu de bicyclette et expliquer pourquoi on observe une élévation de température, chauffage d'un ballon souple rempli d'air à pression constante...

- Expansion dans le vide et diffusion
À la température ambiante T = 300 K, la vitesse quadratique moyenne u d'une molécule de diazote est de l'ordre de 500 m/s (c'est la vitesse d'expansion dans le vide !).
Par contre, la diffusion est lente, même si les molécules vont vite entre deux chocs (le coefficient de diffusion du diazote, à p₀ et T₀ est D₀ = 0,200 cm².s^-1). Pour un gaz, sous 1 bar, à T = 273 K, la valeur de la distance quadratique moyenne parcourue par une molécule dans une marche au hasard est de l'ordre de 1 cm en quelques secondes. Elle est proportionnelle à la racine carrée de la durée.

- Mouvement brownien (1827)
En choisissant une particule de masse élevée, nommée « autre », on visualise le parcours aléatoire d'une particule, résultat des nombreux chocs de la particule avec les autres molécules.
La simulation contribue à donner aux élèves une perception de l'aléatoire, une piste de travail à exploiter en collaboration avec les enseignants de maths et SVT.

Bibliographie

Chomat, A., Larcher, C., Méheut, M. (1990). Modèle particulaire et démarches de modélisation. LIREST-INRP. Paris.

Méheut, M. (1996). Enseignement d'un modèle particulaire cinétique de gaz au collège. Questionnement et simulation. Didaskalia, 8, 75- 96.

Rozier S. (1988). Le raisonnement linéaire causal en thermodynamique classique élémentaire. Thèse, Université Paris 7, L.D.P.E.S.
voir pour un résumé chap.5 dans Viennot L. (1996). Raisonner en physique. Bruxelles : De Boeck.

Pérez J.-P. (1997). Thermodynamique. Fondements et applications. Masson : Paris (2^e édition).

Ogborn J. et coll. (2000). Advancing Physics A2, Ed. by J. Ogborn and M. Whitehouse, Institute of Physics Publishing, Bristol and Philadelphia.