Faire des mathématiques avec l'ordinateur

Il sera utile de comparer les différentes offres actuelles. La construction des figures géométriques est un créneau porteur et on constate une certaine concurrence susceptible de fournir des produits d’un bon rapport/qualité prix. Après les exemples de réalisations, souvent conduites dans des situations priviligiées - enseignants particulièrement compétents et motivés - il faudra se poser la question de la généralisation des usages et des conséquences pédagogiques.

faire des mathematiques avec l'ordinateur

au collège (tome 2) avec disquette - 100 F - au lycée (tome 2) avec disquette - 120 F - Panorama et synthèse des travaux menés dans les académies - CD-Rom "Intégration des technologies nouvelles dans les disciplines : mathématiques - Publications : Direction des Lycées et Collèges - Direction de l'information scientifique, des technologies nouvelles et des bibliothèques.

La première réaction a été de se reporter aux tomes 1 respectifs afin d'observer les évolutions. Plus que le changement, c'est d'abord la continuité qui frappe : préambules analogues sur les différents types d'activités envisageables, liste des logiciels auxquels il est fait référence, liste des logiciels en licence mixte. On observe une présentation plus attrayante, une disquette contenant les fichiers des activités ou figures (mais pas le texte des fiches élèves) et surtout une préface de l'Inspection Générale qui "balise le terrain" et cautionne orientations et hiérarchies.

Trois ans après le premier tome, cette compilation de travaux déjà publiés de ci - de là (et l'EPI en a souvent rendu compte) n'apporte pas une grande innovation pédagogique, mais elle constitue un ensemble de matériaux intéressants. Souhaitons une large diffusion à ces brochures.

 

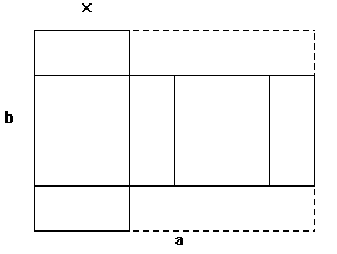
VOLUME D' UNE BOITE PROBLEME Fiche élève   On s'intéressse aux variations du volume d'une boîte parallélépipédique construite en découpant, selon le patron ci-dessous, deux bandes de même largeur dans une feuille rectangulaire de côtés a et b (dans toute la suite on supposera a b). On appelle x la longueur de l'arête indiquée sur le dessin. ACTIVITE PREPARATOIRE Construisez le patron d'une boite parallélépipédique en découpant dans un rectangle de carton deux bandes comme indiqué sur le dessin. PREMIERE PARTIE - FEUILLE CARREE DE COTE 8 On appelle V la fonction qui à x associe le volume de la boîte. 1) Quel est l'ensemble de définition E de V ? 2) Exprimer V(x) pour tout x de E. 3) Calculer la fonction dérivée de V, les valeurs qui l'annulent, tracer le tableau de variation de V et déterminer son extremum. DEUXIEME PARTIE - FEUILLE RECTANGULAIRE Dans toute la suite de l'activité, les calculs et courbes représentatives demandés seront obtenus à l'aide du logiciel Derive. Dans ce cas on peut découper la feuille de deux façons différentes. 1) Précisez les ensembles de définition des fonctions V1 et V2 ainsi définies (pour V1, on prend x sur le côté de longueur a, et pour V2 sur le côté de longueur b). Donnez une expression de V1(x) et de V2(x). 2) On prend a = 8, b = 6. a)Pour chacune des fonctions, calculez sa dérivée, dressez son tableau de variation et déterminez ses extrema. b)Comparez les valeurs obtenues dans les deux cas. c) Faites tracer les courbes représentatives de V1 et V2. Que constatez-vous ? d) Faites une conjecture sur la relation liant V1 et V2. e) Vérifiez la conjecture à l'aide du logiciel. 3) Reprenez les questions posées en 2) avec un autre couple de valeurs de a et b. 4) On veut généraliser les résultats obtenus en e). Faites une conjecture sur une relation liant V1 et V2 (reprenez d'autres valeurs de a et b si nécessaire) et vérifiez la conjecture à l'aide du logiciel (n'oubliez pas de libérer a et b des valeurs précédentes). 5) Reprenez l'un des cas particuliers précédents 2) ou 3). a) Calculez, dans les deux cas pour lesquels le volume de la boîte est maximum, les longueurs des arêtes. Que constatez-vous ? b) Déterminez comment il faut découper la feuille de papier pour que la boîte de volume maximum utilise le moins de papier possible. 6) On veut généraliser les résultats obtenus en 5). a) Vérifiez que V1 et V2 admettent chacune une valeur maximum. b) Déterminez pour quel découpage la boîte de volume maximum utilise le moins de papier.

Nombreux sont les enseignants qui s'interrogent sur les relations entre connaissances/compétences (mathématiques) et les outils (informatiques). Rappeler les objectifs majeurs cités dans les programmes ne répond pas à certaines remises en cause importantes. Par exemple, que devient l'étude des fonctions lorsqu'un "expert" fournit tous les résultats pour peu que l'on sache comment les demander ? L'utilisation de logiciels de calcul formel ne perturbe-t-elle pas certaines acquisitions en matière de calcul algébrique comme les calculatrices altèrent pour certains la maîtrise des opérations ? On peut se demander de façon analogue si les logiciels de constructions géométriques modifieront chez certains élèves l'attitude face à la construction de figures, activité souvent effectuée avec réticence au lycée. Notons que pour l'instant l'utilisation de ces outils se fait dans des conditions favorables - professeurs et élèves volontaires souvent bien motivés. La généralisation ne se fera pas forcément aisément. Face à ces questions, on répond souvent que l'essentiel est dans le SENS donné aux problèmes posés, aux notions introduites, aux étapes de résolution. N'y a-t-il pas lieu d'en savoir plus sur le fonctionnement des outils utilisés et leurs limites. Malgré de nombreuses activités avec la calculatrice, beaucoup de mes élèves de seconde ont cru démontrer à la fin d'un problème de géométrie que 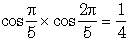avec leur calculatrice, tournant le dos aux résultats établis auparavant. Calculatrice, objet magique !...

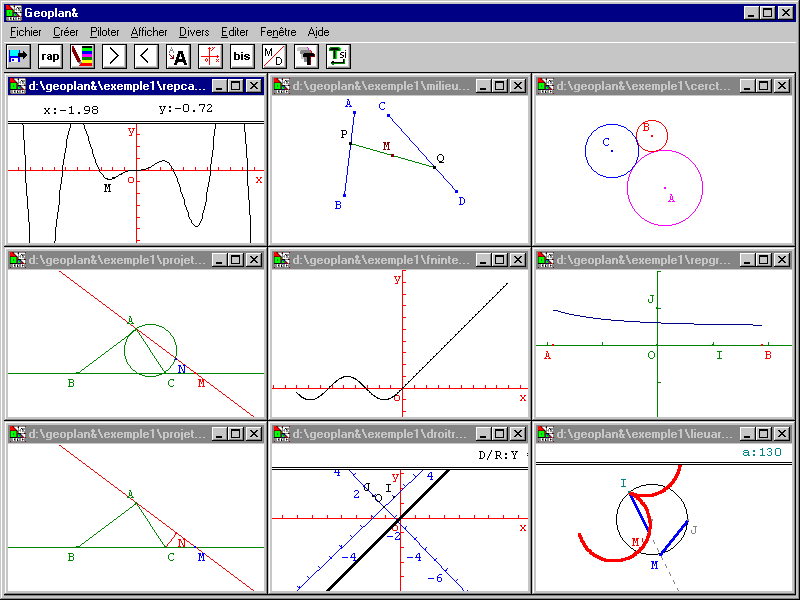
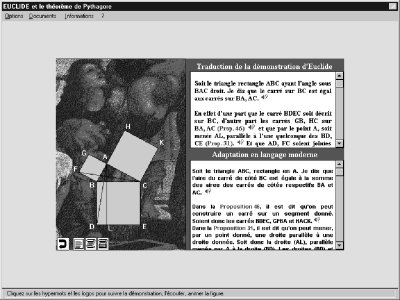
Le CD-Rom est sensiblement plus riche et plus ouvert : outre les brochures mentionnés ci-dessus, il contient une version de démonstration de GEOPLAN sous Windows et de l'encyclopédie Géoflash ainsi qu'une présentation historique du théorème de Pythagore sous Toolbook. On peut regretter que la diffusion limitée de ce produit a priori peu coûteux soit plus une vitrine de l'action d'une équipe qu'un outil permettant de bien informer les enseignants - Quel dommage !

Signalons que GEOPLAN sous Windows en version complète est une excellente réalisation diffusée pour la modique somme de 120 F. Elle mérite d'être largement mieux connue.

Pourquoi ce panorama plus large et plus ouvert ignore-t-il d'autres réalisations et notamment les banques de données diffusées par le CNDP et l'APMEP, les outils d'évaluation développés par la DEP ? Il reste encore de la place sur le CD-Rom... Une deuxième édition enrichie et largement diffusée pour un prix modique serait la bienvenue.

Logiciel de géométrie dans l'espace sous Windows - Ed. Edusoft - prix Camif : monoposte 1410 F, site 2535 F.

Représenter des figures de géométrie dans l'espace selon les règles de la perspective cavalière en faisant varier les points de vue et en éliminant les lignes cachées constitue les points forts de ce logiciel qui a une place assez spécifique dans l'enseignement des mathématiques. La documentation est riche de nombreux exemples disponibles sous Write et représente beaucoup de travail déjà fait facilement récupérable. On retrouvera évidemment des fonctionnalités déjà connues dans d'autres logiciels de constructions géométriques. La cible des utilisateurs est clairement le public lycée et au-delà. On remarquera que si le prix d'une licence est assez élevé, celui de la licence sur site est raisonnable (même si c'est encore beaucoup) pour une application pointue, bien adaptée à des objectifs précis.

On ne parlera pas ici des logiciels permettant de tracer des courbes comme GRAPH’X par exemple, mais des produits concernant d’abord la géométrie, même si on utilise des nombres pour les coordonnées de points ou de vecteurs (pour définir une translation par exemple) ainsi que des mesures -longueur d’un segment, écart angulaire-.

Le plus connu et un des premiers logiciels est sans doute CABRI-GEOMETRE qui continue d’évoluer et de s’enrichir : on le trouve sur la calculatrice TI-92 , sur les micros compatibles PC et sur les Mac.

A l’Atelier de Géométrie peut s’ajouter un volet Multimédia : outre la partie construction de courbes, appelée alors simulateur, on trouvera un ensemble de 15 imagiciels soignés présentant des problèmes sous une forme attrayante (voire spectaculaire) et leur solution progressive à la fois écrite et dite par une voix (masculine ou féminine, au choix !).

GEOPLAN sous Windows, déjà mentionné précédemment pour son excellent rapport qualité/prix propose des fonctionnalités proches, avec une ergonomie légèrement différente : la description des objets est plus textuelle, on nomme les objets plutôt qu’on ne les désigne avec la souris, ce qui évite certaines ambiguïtés. De ce fait, la présentation de l’historique est plus riche.

WINGEOM édité par Pilat Informatique a de nombreuses analogies avec les produits précédents. Il est facile à utiliser comme produit périphérique de Word pour Windows : on insère un objet géométrique comme on insère un objet équation et on dispose de toutes les facilités des liaisons OLE pour le modifier, à moins qu’on ne préfère le sauvegarder en image vectorielle pouvant être retravaillée par le module de dessin (d’autres utilisateurs préféreront utiliser Corel Draw).

Il faudrait encore citer le logiciel HYPOTHESES décrit dans la Revue n°85 de l’EPI dont on trouve une version de démonstration dans la bourse d’échanges de l’EPI. L’accent est mis sur le raisonnement.

On peut donc parler d’abondance de produits. On ressent la nécessité d’une étude comparée plus fine, même si l’on peut dire dès maintenant que tous ces produits sont de bonne qualité et peuvent rendre de nombreux services. On peut aussi se demander quelles seront les conséquences sur le comportement des élèves lorsqu’on en fera une utilisation systématique.

Article paru dans la Revue de l'EPI n° 86, juin 1997.