Possédant deux ordinateurs en classe, j'avais clairement conscience du type de jeux qu'il fallait privilégier : courts (pour permettre le passage de plusieurs enfants), attrayants (mais sans décor trop chargé qui détourne l'attention), à consigne vocale (mais en limitant les bruits et musiques qui perturbent l'entourage).
Nous devions également proposer des exercices qui abordent et font rebondir les notions du programme du cycle 2 (en particulier de Grande Section), et qui présentent une progression sous forme de niveaux de jeux, tout en proposant une évaluation des résultats. Mais avant tout, nous souhaitions mettre l'élève en situation d'acteur, maître de ses choix, face à une situation problème à résoudre avec l'aide du nombre.
 
 

comment jouer ?	tableau précédent	consigne vocale	sortie	tableau  suivant

Pour que l'élève soit entièrement autonome, nous avons sélectionné des icônes (voir ci-dessus) qui reviennent systématiquement dans les jeux et sont expliquées aux élèves à partir du tableau principal des jeux.
Le fait de pouvoir présenter, au fur et à mesure du développement, les exercices aux élèves de ma classe, a permis de les améliorer en tenant compte des réactions, des demandes des enfants et de leur compor-tement. Dans Le repas des gorilles, où il s'agit de ramasser autant de noix de coco que de singes présentés à l'écran, plusieurs élèves ont eu tendance à « foncer », sans même se préoccuper de savoir quelle était la consigne !
Cela laisse supposer qu'ils ont la mauvaise habitude de jouer sans réfléchir ou qu'ils attendent que l'ordinateur passe de lui même à la scène suivante une fois l'objectif atteint. C'est malheureusement le cas de certains jeux dans lesquels l'enfant est incapable de répondre à la question : « As-tu gagné ? » Quel est alors l'intérêt du jeu ?
Dans notre projet, ce n'est pas l'ordinateur qui tient les rênes, mais bien le joueur, qui doit décider seul de passer à la scène suivante une fois le but atteint. Il faut donc impérativement avoir écouté et compris la consigne pour pouvoir agir en ce sens avant de quitter la scène pour évaluer son travail. C'est donc une toute autre démarche qui semble privilégier la réflexion et le raisonnement. 

Dans Le repas des gorilles, l'enfant se trouve face à un tableau présentant des singes. Mais on ne lui dit pas de les compter... c'est à lui de trouver cette solution pour pouvoir ramasser autant de noix de coco. Et là encore, il doit résoudre un nouveau problème : les noix de coco sont groupées en paquets indissociables qui l'incitent à anticiper (il m'en faut 7, je vais prendre 3 et 4 ) et à pratiquer des décompositions additives. 

Dans Le château, il s'agit encore de ramasser « autant », mais il faut d'abord repérer le nombre qui apparaît... et disparaît, puis se déplacer dans un labyrinthe pour collecter les diamants. Il s'agit donc d'être attentif et de pouvoir lire un nombre (avec l'aide de la bande numérique placée près de l'écran). Mais là encore, les enfants sont confrontés à un problème majeur : l'oubli du nombre ! De plus ils doivent trouver une solution : cocher sur la bande numérique, sortir le même nombre de jetons et surtout écrire pour laisser une trace. La stratégie mise en place par l'un ou l'autre est très révélatrice !

En ce qui concerne Profou, les élèves découvrent un robot qui annonce son âge (10, 12, 15 ans selon les niveaux) mais qui n'a pas assez de bougies (par exemple 5). Il faut donc aller chercher le paquet de bougies ou la boîte qui convient pour compléter. Il s'agit encore d'anticiper et de travailler les compléments additifs et le surcomptage. Une fois mémorisée la quantité à rapporter, l'élève dirige Profou à travers un jeu d'arcade où il croise des éléments insolites qui stimulent son imagination. Ainsi, certains ont décidé que le fait de libérer l'esprit de la lanterne magique rend immortel... ou que le dentier qui parcourt le jeu s'appelle Croc Monsieur... 

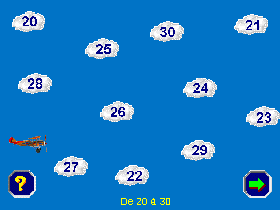
La ballade dans les nuages permet surtout de progresser et de consolider l'apprentissage de la comptine numérique. Les niveaux progressifs : de 1 à 10, de 10 à 20, de 20 à 30, de 1 à 30, de 30 à 1 et enfin, dans le désordre, aident l'enfant à mémoriser la suite des nombres, à associer le nom du nombre à son écriture chiffrée, à identifier un nombre isolé de la comptine... tout en devenant pilote d'avion ou de dirigeable. 

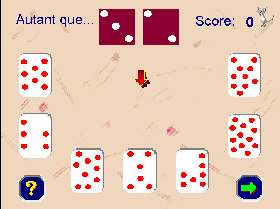
Les autres jeux se jouent à deux, chacun son tour. La motivation s'en trouve accrue, car les bonnes réponses augmentent les scores qui seront comparés en fin de jeu. Les objectifs reprennent les comparaisons de quantités par le travail des notions « autant » et « moins ». Il s'agit de désigner une carte contenant autant de points que le dé chiffré (associer l'écriture du nombre à la quantité) ou que les 2 dés à constellations (prendre conscience que la disposition n'influe pas sur la quantité).

Dans « moins que », l'élève doit faire preuve de stratégie et choisir la carte contenant le plus de points pour arriver au score gagnant. Et dans « inférieur à », il doit désigner tous les nombre inférieurs à celui du dé. Les nombres choisis (26, 30, 43, 25, 70) peuvent sembler difficiles à lire pour des enfants de GS, mais c'est à la requête de plusieurs d'entre eux, demandeurs de grands nombres, que nous avons répondu.
Les élèves disposent d'une bande numérique pour identifier ces nombres moins connus et chercher leur emplacement sur la bande. Ils repèrent ainsi des constantes dans la suite écrite des nombres. Ils apprennent aussi à ne pas confondre des graphies proches (12 et 24).

Après quelques années de test et d'observation des élèves, et en toute modestie, il apparaît que ces exercices sont une activité à part entière et permettent d'utiliser l'atelier informatique au même titre que les autres ateliers de la classe. Le fait d'avoir à répondre à une consigne précise en organisant soi-même la démarche : tâtonnement, dénom-brements répétés, écriture du nombre pour ne pas oublier, aide de la bande numérique ou de jetons, anticipation et même calcul mental, oblige l'élève à faire des hypothèses et à prendre des décisions actives. (Ce qui peut aussi se révéler intéressant en phase d'évaluation.)

Il utilise ainsi ses capacités de raisonnement, de mémoire, de stratégie. Et il devient aussi plus autonome. C'est, pour la plupart des élèves, une activité plus attrayante et moins soumise à « sanctions » qu'un travail sur papier qui laisse une trace. L'informatique peut aussi aider au déblocage de réticences dans certaines situations où l'explication reste incomprise. L'enfant reprend confiance au lieu de s'installer dans l'échec. Mais il se produit aussi, devant l'ordinateur, des échanges, des discussions concernant le choix de la stratégie, ou une compétition positive (pour les jeux à 2). L'enfant n'est pas isolé devant la machine, c'est également un lieu de communication, qui peut se révéler très riche et bénéfique aux élèves.
Notre rôle d'enseignant est de tout mettre en œuvre pour permet-tre l'égalité des chances et la diversification des situations d'appren-tissages. Dans cette optique, l'accès des enfants à l'informatique n'est plus contestable aujourd'hui.

Ces logiciels fonctionnent sous Windows 95/98 et NT. Configuration minimum : PC Multimédia 486 (Pentium recommandé) avec lecteur de cédérom et carte son - 16 Mo de RAM - Carte graphique 2 Mo (256 couleurs). 
Les jeux peuvent être lancés depuis le cédérom ou installés sur le disque dur, auquel cas ils nécessitent 35 Mo de libres. 
Ce produit, disponible courant juin 1999, est diffusé par l'EPI au prix de 80 F TTC, port compris. Bon de commande.