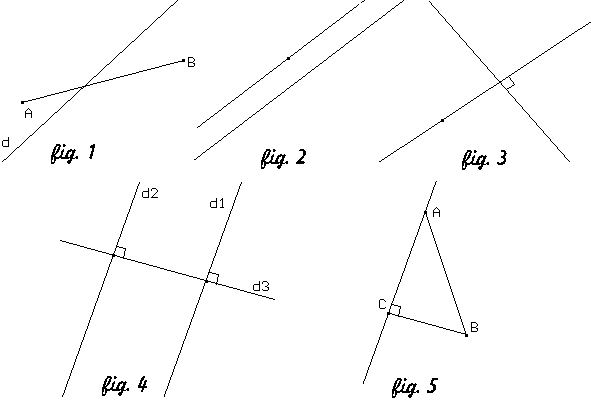
INTRODUCTION

Ma reconversion du métier d'ingénieur en informatique au métier de professeur des écoles n'est pas étrangère au choix du sujet de mon mémoire de 2^ème année d'IUFM. L'ordinateur étant devenu pour moi un outil de travail quotidien au même titre que le crayon et la gomme, je me suis naturellement posé la question de savoir quelle pourrait être son utilité à l'école.

Les instructions officielles qui recommandent l'utilisation de l'informatique ont trois objectifs principaux 

La découverte de CABRI géomètre présent dans l'école dans laquelle j'ai utilisé mon crédit individuel de formation m'a incitée à expérimenter l'utilisation de celui-ci auprès d'une classe de CM1 afin de voir s'il pouvait aider les élèves à clarifier les concepts de géométrie et les aider à passer plus facilement à l'abstraction.

Cet article présentera une synthèse de la partie de ce mémoire consacrée à l'expérience pratique sur le terrain. 

1. Les logiciels de géométrie

1.1. Les Environnements Interactifs d'Apprentissage avec Ordinateur (E.I.A.O)

On peut constater un développement des EIAO dans l'enseignement des mathématiques. Les EIAO utilisés dans l'enseignement de la géométrie sont des logiciels de construction géométrique. Ces EIAO sont des micro mondes constitués d'objets de base (points, droites, cercles) et de primitives de construction (ex. : traçage de la perpendiculaire à une droite passant par un point donné.)

1.2. Un EIAO particulier : " Le géomètre "

1.2.1. Présentation du logiciel

" Le Géomètre, le CAhier de BRouillon Interactif pour un nouvel apprentissage de la géométrie (CABRI) " a été développé au laboratoire de Structures Discrètes et de Didactique (IMAG) au CNRS de l'Université Joseph Fourier de Grenoble. Il est, sans doute, le plus connu et le plus répandu de ces types de logiciel. On le trouve sur micro-ordinateurs compatibles PC, sur Macintosh et sur certaines calculatrices. Il est à noter que ce logiciel a été développé à destination d'élèves du secondaire. Toute la documentation consultée sur ce sujet ne fait état que d'expériences dans des classes de collège et de lycée et, à ce titre, ma problématique est donc sensiblement différente.

1.2.2. Analyse du fonctionnement

Deux caractéristiques importantes de cet environnement informatique résident dans la coexistence de primitives de dessin pur et de primitives géométriques et dans la manipulation directe du dessin. Si l'on déplace à l'aide de la souris un des éléments de base du dessin, celui-ci se déforme en respectant les propriétés qui ont servi de base à sa construction. Si un dessin a été réalisé à partir de primitives de dessin pur c'est à dire au jugé, il perd ses propriétés spatiales apparentes dans son dessin original lors du déplacement d'un de ses éléments. Par exemple, si un parallélogramme est construit à l'écran à partir des primitives de dessin pur, le déplacement de l'un de ses sommets le transforme en quadrilatère quelconque. S'il a été construit en utilisant les primitives géométriques (tracé de côtés parallèles ou tracé des milieux des diagonales), le déplacement de l'un de ses sommets provoque la modification de ses angles ou de la longueur de ses côtés mais la figure reste un parallélogramme. Les propriétés attribuées à un objet parce que lues sur un dessin statique le représentant ont de fortes chances de n'être apparemment plus vérifiées lors de la déformation du dessin. L'exigence de communiquer au logiciel un procédé géométrique de construction permet ainsi de caractériser l'objet géométrique. Le logiciel a été conçu avec l'idée que ce passage par les primitives géométriques devrait favoriser l'usage de connaissances géométriques. D'autre part, le champ d'expérimentation dans le dessin papier crayon est limité pour des raisons matérielles (imprécision du tracé, impossibilité de rendre temporairement invisible une partie du dessin, limitation du nombre d'objets à gérer). " Le géomètre " élargit donc le champ d'expérimentation possible. Dans le contexte papier crayon, l'élève peut tourner sa feuille et voir le dessin dans différentes positions mais il ne peut en faire varier les éléments variables qu'en réalisant un nouveau dessin. Au contraire, l'utilisation du logiciel en autorisant le déplacement des objets, permet à l'élève d'exercer des rétroactions externes à lui-même et indépendantes de l'enseignant : elles sont ainsi susceptibles de le faire évoluer. C. Laborde et B. Capponi  inventorient les différentes manières de faire travailler les élèves avec " le géomètre " en analysant les différents types d'entrées pouvant leur être communiquées, les différentes sorties pouvant être demandées et les tâches correspondantes à effectuer. Celles-ci peuvent être résumées dans le tableau ci-après :
 
 

1.3. De la théorie à la pratique

L'étude pratique que j'expose ci-après m'a permis de confronter les différentes théories consultées (cf. bibliographie) à la réalité d'une utilisation du logiciel " le géomètre " à l'école élémentaire. 

2. La pratique

2.1. Utilisation du logiciel en classe

2.1.1. Contexte de l'expérimentation

La version de logiciel utilisée pour la réalisation de mon mémoire et les applications pratiques associées est la version 1.6, sous copyright NATHAN logiciels / CNRS 1988-89 pour PC.

L'étude a été menée dans une classe de CM1 d'un bon niveau moyen. Quatre élèves peuvent être toutefois considérés comme en difficulté, deux d'entre eux sont suivis par le réseau d'aide. La classe est partagée en deux groupes pour cette activité. Les deux groupes se succèdent en salle informatique et les mêmes séquences sont donc menées deux fois. Il faut toutefois noter que bien que partagés naturellement par affinités, les deux groupes n'en sont pas moins deux groupes de niveaux. Les consignes en sont considérablement allégées et le travail plus rapide dans le groupe " fort ". L'école possède six licences pour ce logiciel et les élèves travaillent donc à deux ou trois par PC. L'informatique est une pratique habituelle dans cette école et les enfants sont tous habitués au maniement de l'ordinateur, ce qui m'évite les séquences préalables d'appropriation du matériel.

2.1.2. Progression

Elle est composée de deux phases principales :

J'ai choisi de reprendre en détail ci-après les séquences 1, 2, 3 et 7 qui m'ont semblé les plus intéressantes quant à ma problématique.

2.1.3. Déroulement

L'objectif principal de la 1^ère séquence est l'appropriation du logiciel par les élèves. Les productions sont libres, les explications sur l'utilisation du logiciel succinctes. Il est intéressant de noter que les élèves font preuve d'une grande créativité et réussissent à détourner l'outil de son rôle initial pour en faire un outil de création graphique. Cette première manipulation les contraint à se poser les questions précises concernant le vocabulaire. A titre d'exemple, ils se posent la question de savoir comment " faire un trait ". En effet, un outil géométrique ne trace pas des " traits " mais des segments ou des droites, cela les contraint donc à s'interroger sur le terme précis qui permettra de construire " un trait qui ne dépasse pas de l'écran " (un segment !).

L'objectif de la 2^nde séquence est un renforcement des notions de parallèles et perpendiculaires qui ont déjà été étudiées en classe de manière classique. Il s'agit ici de suivre une procédure écrite. Les élèves doivent tracer un segment, des droites parallèles et perpendiculaires à ce segment, reconnaître les situations de parallélisme et d'orthogonalité (avec justification, si possible). En fin de séquence, les élèves impriment leurs productions et vérifient avec leur instrument habituel (équerre), ce qui permet de faire le lien entre les outils " classiques " et ce nouvel outil.

Pour reprendre l'analyse des différents registres utilisés de C. Laborde et B. Capponi, nous sommes ici dans la configuration suivante :

Tâche pour l'élève

La fiche de consignes fournie à chaque groupe oblige à une démarche intellectuelle en trois étapes :

Il ressort de cette séquence que quelques notions sont encore incertaines, voire non acquises. Les notions de segment/droite et parallèle / perpendiculaire sont confuses pour nombre d'élèves. Les productions à partir de la procédure décrite sur la fiche sont, en majorité, bien réalisées. La reconnaissance des caractéristiques géométriques (parallèle ou perpendiculaire) est moins bien réussie. Il existe toujours une confusion entre les deux notions. Les justifications sont, sauf exceptions, inexistantes ou ne reprennent que les propriétés des notions (" les droites sont parallèles parce qu'elles ne se touchent jamais ").

L'objectif de la 3^ème séquence est le réinvestissement du vocabulaire précis dans une production. Les figures proposées permettent une réutilisation des notions de droite, segment, parallèle et perpendiculaire. Des schémas sur papier sont fournis aux élèves qui doivent les reproduire à l'écran. Je précise que les objets doivent supporter le déplacement : les parallèles et les perpendiculaires doivent le rester lors des déplacements des points qui ont servi à les construire.

A l'inverse de la séquence 2, les élèves doivent imaginer la procédure leur permettant de réaliser les figures proposées. Nous sommes ici dans la configuration :
 

Tâche pour l'élève

 Observations

Lorsque les élèves ont réalisé leur figure ils ne pensent pas d'eux-mêmes à déformer la figure pour s'auto-valider. Je contrôle donc avec eux la production en leur faisant varier les paramètres de départ et les amène à constater l'erreur s'ils ont construit " à l'œil " en utilisant les primitives graphiques de l'outil (évaluation approximative d'un angle droit ou d'une parallèle : l'équerre est parfois utilisée, posée sur l'écran !). J'exige une production correcte pour passer à l'exercice suivant. Ceci me permet de reprendre et d'observer chaque élève individuellement.

Les notions suivantes sont toujours confondues et/ou mal utilisées : segment/droite et parallèle/perpendiculaire.

Lors de la 7^ème séquence, nous étudions un quadrilatère particulier : le parallélogramme. L'objectif est de découvrir que, par transformation, un parallélogramme peut devenir un rectangle, un losange et/ou un carré. Il s'agit cette fois de notions nouvelles. Les enfants commencent à bien connaître le logiciel et sont disponibles pour les nouvelles acquisitions. Un parallélogramme de type prototypique est tracé sur tous les écrans préalablement à la séquence. Une feuille de consigne est distribuée.

Nous sommes ici dans la configuration :
 

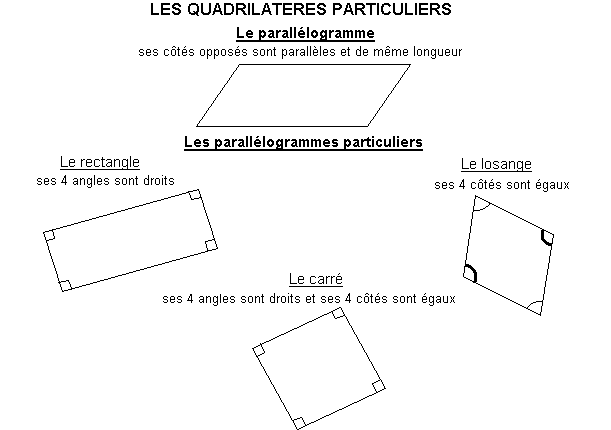
Tâche pour l'élève

Les élèves doivent observer le quadrilatère à l'écran et ses caractéristiques (cotés égaux et parallèles deux à deux). Ils doivent ensuite le déformer pour obtenir des quadrilatères particuliers :

Observations

La séquence se déroule avec beaucoup de facilité pour les enfants. Ils connaissent maintenant l'outil et sont motivés par une utilisation différente de celle qu'ils en ont fait jusqu'à présent. Tous les groupes parviennent à effectuer les manipulations. On peut noter que celles-ci sont très fines et un peu délicates à réaliser : il faut être précis dans ses mouvements pour réaliser un angle droit et cela s'avère difficile pour certains. Des cas plus particuliers que prévu se présentent : lors de la déformation du parallélogramme de manière à obtenir ses quatre côtés égaux, les angles se trouvent être des angles droits et les élèves arrivent donc à la conclusion (trop rapide) qu'il s'agit d'un carré sans être passés par l'étape " losange " que j'aurais souhaitée. Le groupe des élèves les plus faibles réalise l'exercice en 35 minutes, le groupe des plus forts en 25 minutes. L'évaluation des acquis réalisés à partir de cette séquence de découverte sera faite dès la séquence suivante lors d'une évaluation formelle en classe avec les instruments " classiques ".

Cette séquence représente un des cas spécifique dans lequel l'utilisation du logiciel est intéressante : utiliser la déformation de figure à partir des points de base sans modifier les propriétés ayant servi de base à la construction (parallélisme des côtés deux à deux). C'est évidemment le cas typique d'une manipulation impossible sur papier. Elle pourrait être assimilée à la manipulation consistant à superposer deux bandes de papier à bords parallèles, le parallélogramme étant constitué par l'intersection des deux bandes. Mais sur l'écran, les mesures de longueurs et le marquage d'angle s'affichent automatiquement, ce qui permet une validation immédiate de la figure.

2.1.4. Principaux problèmes rencontrés lors des séquences

Un des problèmes rencontrés dans l'utilisation du " géomètre " est l'obligation de décrire un point comme l'intersection de deux objets pour pouvoir être utilisé. Par exemple, le point d'intersection de deux droites sécantes doit être défini comme tel avant de pouvoir être utilisé comme point de base d'une autre construction. Ceci est extrêmement déroutant pour de jeunes enfants : lorsqu'on trace deux droites sécantes, l'existence d'un point à leur intersection est une évidence géométrique implicite. Il faut noter que cette contrainte n'existe plus dans les versions plus récentes du logiciel.

Un autre problème est que ce logiciel est largement supérieur au besoin de l'école élémentaire, mais cet inconvénient est facilement résolu par le paramétrage des menus qui permet de supprimer ce qui " pollue " les menus pour des jeunes élèves.

2.2. Les évaluations

Une 1^ère évaluation des compétences géométriques est réalisée après 4 séquences sur ordinateur. Cette évaluation est volontairement réalisée sur papier et en classe de manière à évaluer individuellement et de manière " classique " les compétences des élèves. Elle est composée des éléments suivants :

La 2^nde évaluation sert à vérifier les acquis réalisés au cours de deux séquences et sur ordinateur seulement. Comme la première, cette évaluation est réalisée en classe, sur feuille.

Le bilan de l'évaluation est très positif. Beaucoup de notions sont comprises. Un bon nombre d'élèves apporte une réponse correcte à la dernière question : " je suis à la fois losange et rectangle, qui suis-je ? " Il est extrêmement intéressant de noter qu'un enfant habituellement en grande difficulté réussit très bien ce contrôle. A contrario, une élève habituellement brillante échoue gravement.

2.3. Le point de vue des élèves

Une enquête réalisée à la fin de la seconde évaluation auprès des vingt-sept élèves de la classe fait apparaître que leur point de vue est assez unanime sur l'utilisation du logiciel : vingt élèves (74%) ont trouvé la géométrie plus facile avec le logiciel. Les raisons invoquées en sont clairement (pour dix d'entre eux) que cela les affranchit des problèmes de matériel (papier/crayon) et de traçage. Deux élèves invoquent l'intérêt de la possibilité de déformation des figures pour valider leur production, un autre apprécie que l'ordinateur " possède sa propre équerre ".

Parmi ceux qui ont trouvé la géométrie plus difficile avec le logiciel (trois élèves), l'une explique qu'" elle sait mieux ce qu'elle fait à la main ", les autres ne justifient pas leur réponse.

Vingt et un élèves (78%) déclarent avoir aimé les séances, parmi eux, sept disent spontanément aimer la géométrie (la géométrie ou la géométrie sur ordinateur ?), cinq disent aimer travailler sur ordinateur. Il apparaît de manière sous-jacente dans les réponses que les élèves n'ont pas l'impression de travailler lorsqu'ils sont en salle d'informatique. Certains disent avoir été gênés par le travail en équipe de deux ou trois sur chaque ordinateur, d'autres trouvent au contraire cette situation favorable. Une élève s'est sentie gênée par le bruit produit par l'ordinateur lorsqu'elle faisait une erreur (bip sonore).

Sur la compréhension des notions, les réponses sont partagées sur les notions de droite, segment et parallèle. Ces notions ayant déjà été étudiées auparavant, certains enfants ne voient sans doute pas ce qu'ils ont acquis de plus. La notion de perpendiculaire est ressentie comme mieux comprise par dix-huit élèves (67%). Vingt-quatre élèves (89%) déclarent avoir compris les notions liées aux quadrilatères particuliers. Il s'avère que l'une des deux élèves déclarant ne pas avoir compris la notion est celle ayant échoué à l'évaluation. Elle déclare par ailleurs n'avoir aimé que les séances au cours desquelles elle a pu réaliser des dessins librement.

3. CONCLUSIONS

3.1. La confrontation textes - pratique

3.1.1. En ce qui concerne les programmes et les textes

J'ai pu, lors de cette expérience, constater que le logiciel permet de répondre à différents points des textes concernant l'apprentissage de la géométrie :

3.1.2. En ce qui concerne les difficultés d'apprentissage

Il serait tout à fait prétentieux de tirer des conclusions d'une si courte expérience concernant un seul cas d'enfant en difficulté, mais j'ai trouvé tout à fait encourageant de voir la réussite dans l'acquisition d'une nouvelle notion de cet élève habituellement en échec. Je pense, comme Guy Harlin qui l'utilise pour la rééducation des élèves en difficulté, que cette utilisation de l'ordinateur qui n'est pas rattachée pour eux à des expériences négatives (pour le moment !) est porteuse d'espoir. A contrario, le fait d'avoir constaté qu'une élève habituellement brillante semblait avoir été gênée par cette nouvelle approche montre bien qu'il ne s'agit en aucun cas d'un outil universel destiné à détrôner les autres ! Il ne s'agit que d'un outil complémentaire.

3.1.3. En ce qui concerne les constats d'autres expériences

Comme J.F. Canet, C. Laborde et B. Caponi, j'ai pu constater que le logiciel permet de mieux appréhender la notion de figure géométrique. Il aide, en effet, à dissocier la notion de dessin de la notion de figure géométrique. Pour P. Bernat, " cet environnement apporte aux figures géométriques une nouvelle dimension : le mouvement et l'animation interactive du dessin " . Le logiciel apporte de ce fait une dimension expérimentale plus difficile à obtenir dans une situation papier/crayon. Je me suis largement inspirée pour la réalisation de ce mémoire et des séquences de classe des travaux de C. Laborde, B. Caponi, P. Bernat et R. Cuppens.

En cycle 3, il semble que les enfants ne possèdent pas la maturité suffisante pour s'auto-valider en prenant l'initiative de déformer la figure pour vérifier la validité de leur construction. Cette validation par déformation a été, en règle générale, réalisée en ma présence ou à ma demande. On peut aussi penser que ces huit séquences (dont six seulement en salle informatique) ont été insuffisantes pour créer ce type d'automatisme.

3.2. Prolongements à envisager

Je souhaite pouvoir utiliser à l'avenir un tel outil tout au long d'une année scolaire (ou même du cycle 3), mais de manière moins systématique, en renforcement de notions acquises en classe ou pour des phases de découverte à prolonger en classe, mais sur l'ensemble du programme Je regrette de ne pas avoir eu le temps de l'expérimenter en particulier pour un travail sur les symétries.

3.3. Conclusion générale

Les séquences ont été agréables à réaliser avec des enfants motivés et intéressés. La pratique, en salle informatique, est différente de la pratique de classe, l'ambiance y est différente. On peut remarquer que le travail sur ordinateur est très motivant pour les enfants, celui-ci étant toujours associé à la notion de jeu. Les élèves se sont montrés très créatifs lorsque cela leur a été demandé lors des séquences 1 et 6.

Au premier abord, l'ordinateur apporte plus une contrainte qu'une aide à la production, mais, en obligeant à une grande rigueur il permet une compréhension plus fine des notions et oblige à une acquisition précise du vocabulaire.

L'ordinateur permet de dissocier l'habileté manuelle de l'élève nécessaire pour réaliser des figures géométriques sur papier de ses connaissances mathématiques : avec les instruments classiques, le manque de soin dans la réalisation de la figure peut bloquer le raisonnement mathématique qui en découle. " Le géomètre ", quant à lui, trace fidèlement ce qui lui est demandé, sans erreur : par exemple, une droite forme dans tous les cas un angle droit avec la droite à laquelle elle a été définie comme perpendiculaire : il ne peut y avoir d'erreur de traçage due à un mauvais positionnement de l'équerre. Ceci implique de ne pas omettre d'enseigner en classe cette utilisation des outils qui serait absente dans le cas d'une utilisation systématique du logiciel.

En ce qui concerne l'évaluation de la figure produite, ce n'est pas le maître qui donne son verdict : l'enfant voit de lui-même les erreurs éventuelles lorsqu'il déforme la figure ou que l'ordinateur émet un bip sonore lorsque l'enfant demande une construction illicite (même si ce " bip " est ressenti comme agressif pour certains !).

Malheureusement, le cadre du crédit individuel de formation qui permet aux PE stagiaires d'intervenir ponctuellement dans une classe dans le cadre de leur mémoire est bien trop réducteur pour évaluer complètement l'intérêt de ce produit à l'école élémentaire. Ces premières conclusions m'amènent à résumer ainsi ses principales qualités :

BIBLIOGRAPHIE

Ouvrages référencés :

· Bernat Philippe - Évaluation et évolution d'un logiciel de géométrie dynamique - Revue REPERES IREM, Juillet 97, n° 28, p.9-36.
· Canet J.F., - Informatique et enseignement des mathématiques, le temps de la maturité ( ?) - La revue de l'EPI , Septembre 94, n° 75 - p. 153 - 162.
· Cuppens Roger- Quelques réflexions sur le logiciel CABRI Géomètre - Brochure APMEP, 1996, n° 402.
· Développement de l'informatique dans l'enseignement : circulaire n°86-330 du 3 Nov. 1986 - R.L.R n° 525-7, 1989 - p. 39-40.
· Guinet Raymond - Le point sur l'informatique à l'école - Revue grand N, 1993, n° 51-p. 85-89.
· Harlin Guy, - L'ordinateur, un outil pour la rééducation - La revue de l'EPI, Décembre 96, n° 84 - p. 61-67.
· Informatique et nouvelle politique pour l'école primaire : circulaire n°91-117 du 14 Mai 1991- R.L.R. n° 514-5 - p. 191-198.
· L'équipement informatique des écoles élémentaires : circulaire n°87-319 du 14 Octobre 1987 - R.L.R. n° 514-5 - p. 190-191.
· Gauthier Michel - L'ordinateur : Enseignant, examinateur ou pédagogue ? - La revue de l'EPI , Juin 96, n°86 - p.73-83.
· Laborde C., Capponi B.- Cabri géomètre constituant d'un milieu pour l'apprentissage de la notion de figure géométrique - Recherche en didactique des mathématiques Volume 14/1.2,1994, n° 40/41, Grenoble : La pensée sauvage, p. 167-209.
· Mathématiques - articulation école collège : note de service n° 96-279 du 29 novembre 1996 - B.O.E.N., 5 décembre 1996 - p. 2946-2951.
· Ministère de l'Éducation nationale, Direction des Écoles - Programmes de l'École primaire - 1^ère éd. - Paris : CNDP, Savoir Lire, 1995.
· Orientations pour l'informatique dans l'enseignement : lettre du 29 Oct. 1985 -R.L.R. n° 525-7, 1989 - p. 37-39.
· Utilisation des équipements informatiques des écoles élémentaires : circulaire n°87-160 du 11 Juin 1987 - R.L.R. n° 514-5 - p. 185-189.

Ouvrages consultés :

· Cuppens Roger- Faire de la géométrie en jouant avec Cabri géomètre Tome 1- Brochure APMEP, 1996, n° 104.
· Enseignement, formation et nouvelles technologies - Les Dossiers de l'Audiovisuel - Septembre-Octobre 1997, Numéro spécial 75 - Bry sur Marne : INA publications.
·Le Géomètre : Manuel de l'utilisateur- Paris : Nathan, Août Septembre 1989- 78 p. (Nathan Logiciels).
· Versini Anny, Versini Jean-Marc, Ordinateur et pédagogie différencie - Paris : Nathan, 1996 - p. 89-94.