|
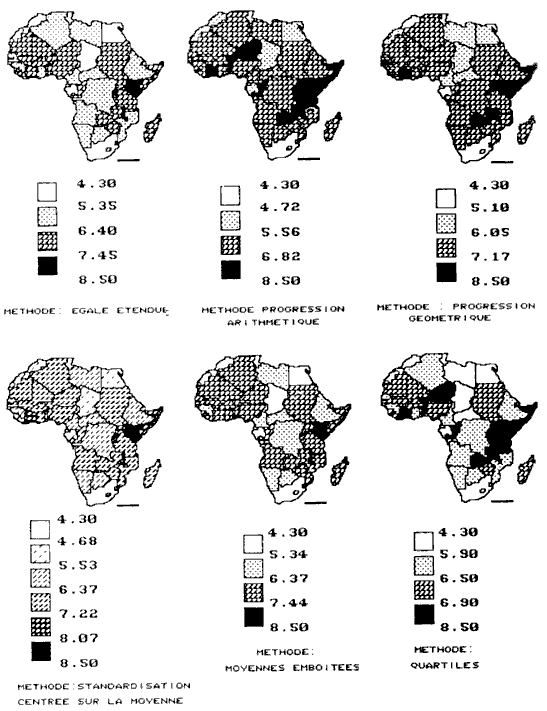
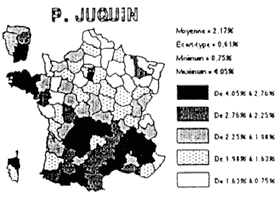
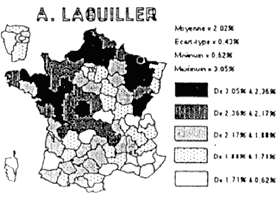
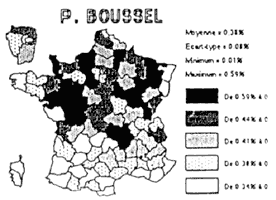
Cartographie et traitement informatisé des données, Claude Loudenot Depuis une décennie le statut de la carte a totalement changé. La carte est devenue un moyen de transcrire aussi bien des séries de données statistiques que de figurer des flux. La carte « image » a fait place à la carte modèle analytique. Dans le même temps, la cartographie est passée des pages glacées des atlas ou des manuels de géographie aux journaux à grands tirages dont elle fait souvent la une. La carte « à jeter » a ainsi remplacé la carte à voir. En même temps qu'elle se vulgarisait, son champ de représentation s'élargissait démesurément. Il n'y a qu'à feuilleter les pages d'un grand hebdomadaire, quelque qu'il soit, voire d'un quotidien, pour s'apercevoir que la représentation cartographique est partout et que tout devient cartographiable. Parallèlement, la carte a acquis ses titres de noblesse en devenant l'outil privilégié des décideurs et des aménageurs. La véritable révolution épistémologique qu'a connu la géographie, prise comme une science sociale, tout comme les possibilités offertes par une nouvelle génération d'ordinateurs ont contribué largement à cette transformation. Face à une telle surabondance on peut légitimement se poser la question fondamentale de la fiabilité de ces cartes informatisées, question d'autant plus importante que ces cartes sont devenues les pivots d'argumentations et d'analyse de phénomènes que les séries statistiques seules ne peuvent mettre en évidence avec la même acuité. Là où l'oeil ne perçoit que des successions de chiffres, sans en distinguer toujours clairement, et pour cause, le message, la carte, issue de ces mêmes données, semble apporter des réponses évidentes qui littéralement sautent aux yeux. L'oeil, tout entier absorbé par le message du codage, dédaigne trop souvent la légende qui l'accompagne. On peut dès lors, pour peu que l'on compare deux ou plusieurs cartes, commettre les pires erreurs d'interprétation. En fait la transformation de données statistiques en cartes, qu'elles soient par plages ou par points proportionnels, pose à différents niveaux de sérieux problèmes qui doivent être connus sous peine d'arriver, sans s'en apercevoir, à des interprétations complètement erronées. Il est finalement facile de faire dire aux chiffres tout et le contraire, cela nous le savions déjà ; la représentation cartographique ne fait qu'amplifier le phénomène. À un premier niveau, les données elles-mêmes sont en cause. Ce n'est pas parce que l'on a devant soi un tableau de données statistiques que l'on pourra pour autant arriver à une représentation cartographique. Les données, lorsqu'il s'agit d'une série, doivent être continues, à la fois dans le temps et dans l'espace. Toute série lacunaire pose problème. Leur objet doit être le même, il doit y avoir cohérence interne. Même si, en apparence tous ces critères sont réunis, se pose toujours le problème de l'origine des données et de leur fiabilité. À cet égard bien des statistiques, émanant d'organismes officiels sont douteuses et doivent être prises avec beaucoup de précaution. Qu'il s'agisse de raisons d'ordre politiques ou de la simple impossibilité d'avoir des paramètres de recensement adéquats, les pires écarts dans une évaluation chiffrée d'un phénomène sont possibles. Les épidémiologistes savent depuis longtemps que les chiffres de morbidité annoncés par certains pays sous développés ou en voie de développement peuvent varier de 1 à 100, parfois plus, et relèvent de la plus haute fantaisie. Mais on prend moins garde à des dérives tout aussi considérables dans le domaine de l'économie ou de la population. Dès lors, comment, à partir de données fausses, arriver à une représentation cartographique exacte ? Il importe par ailleurs, avant de se décider à transformer les données en des représentations visuelles, de réfléchir à la forme que celles-ci prendront. Parfois une ou des représentations graphiques seront plus significatives qu'une carte, parfois, les deux formes seront nécessaires. En fait, dans cette forme de traitement de données statistiques, le choix n'est jamais arbitraire mais il doit correspondre à la meilleure manière de mettre en évidence la problématique choisie et de la confirmer. Une carte n'est jamais "innocente" et ce type de cartes encore moins que les autres. R. Gimeno, lorsqu'il présente les principes de la graphique à ses étudiants, a coutume de prendre l'exemple de l'Uruguay, mais nous pourrions aussi bien prendre l'exemple de la France. Dans les deux cas, lorsque nous voulons représenter la répartition de la population, nous sommes gênés par la répartition des données. Le nombre d'habitants de Montevideo, tout comme celui de l'agglomération parisienne, par leur importance, dénature totalement la répartition des habitants. Si le choix se porte sur une représentation cartographique, ces deux exemples vont mettre en évidence de manière éclatante un nouveau problème spécifique à la représentation cartographiques de données numériques, à savoir le découpage en classes (discrétisation), et la répartition de l'ensemble des données entre ces différentes classes. C. Cauvin [1] a bien montré qu'il y avait une bonne dizaine de méthodes de discrétisation et que toutes ces méthodes étaient scientifiquement exactes, même si elles correspondaient à des représentations présentant des différences sérieuses. Prenons le cas de l'Afrique développé dans l'exemple 1. Il est clair que toutes les cartes traitées sont parties d'un tableau de données identiques. Le choix de la carte à retenir se fera en fonction de la problématique de départ et de l'objectif que l'on assigne à la carte. Un autre aspect mérite attention et peut devenir, consciemment ou non, le point de départ de démonstrations erronées. Il s'agit cette fois du choix fait entre la possibilité de transposer un tableau tel quel et celui de traiter les données avant que de les transformer en une représentation cartographique. Prenons le cas, par exemple, du nombre d'étrangers par rapport à la population totale d'une commune recensés en 1982 et en 1990. Pour une commune de 100 habitants le nombre d'étrangers peut être passé de 0 à 10, alors que pour une autre comptant 10 000 habitants, il sera passé de 500 à 510. La représentation sera totalement différente selon que l'on cartographie les données absolues (dans les deux cas il y a une augmentation identique de 10 unités), ou que l'on représente le taux d'augmentation des étrangers par rapport à la population totale. L'exemple choisi ici est volontairement caricatural, mais nous tombons dans le même travers à propos de cas qui peuvent paraître normaux à quiconque ne réfléchit pas suffisamment. (cf. exemple 2). Il est bon également de se méfier de la notion de "moyenne" présente dans beaucoup de statistiques. La densité moyenne de population d'un pays est-elle un indicateur suffisamment précis de la répartition de la population ? Quelle est la signification de revenu moyen, voire de PNB par habitant, dans certains pays en voie de développement où nous savons pertinemment que le rapport entre les revenus des plus riches et des plus démunis peut varier de 1 à 100. La règle veut que l'on essaye, toutes les fois où les données le permettent, d'aller vers une représentation la plus fine possible au niveau de l'espace. Pendant longtemps, pour l'Europe par exemple, n'ont figuré, dans les manuels et les atlas, que des cartes par pays. La pratique actuelle de travailler à l'échelle régionale donne une toute autre représentation de l'espace européen. (exemple 3). Jusqu'à présent nous n'avons évoqué que le cas d'une carte unique. Restent les problèmes associés à la mise en relation de deux ou plusieurs cartes, dans ce dernier cas on parlera de collections de cartes. Compte tenu du codage choisi dans les cartes par plages, la plage « noire » exprime toujours la classe des plus fortes valeurs, de même que la plage blanche ne représente pas l'absence de valeurs, mais la classe des plus faibles valeurs. Dès lors, pour peu que l'on n'y prenne garde, l'oeil jouant en l'occurrence le rôle de sélecteur naturel, seul la masse noire perçue est prise en compte, sans que l'on ait toujours le souci de lire la légende correspondante. La preuve est donné par cet exemple classique présenté par R. Gimeno pour les élections présidentielles de (exemple 4). Dans la première collection de cartes chaque candidat est représenté avec le pourcentage de voix obtenues. En soi ces cartes ne sont pas fausses à conditions qu'elles soient prises chacune individuellement et que l'analyse ne se porte pas vers une comparaison des cartes entre elles. La comparaison est en effet impossible du fait, que si ces cartes sont à la même échelle spatiale et que, même si elles comportent un nombre de classes identiques, les seuils de répartition sont différents. Le seul moyen de comparer est, dans ces conditions, d'attribuer une échelle commune de discrétisation à l'ensemble des cartes qui constituent la collection. Nous en sommes restés, jusqu'à présent, dans la logique d'une représentation cartographique qui n'utilise que la palette du noir au blanc. Mais bon nombre de logiciels de cartographie, permettent, à l'heure actuelle, des réalisations en couleurs qui font merveille et séduisent. Il importe encore plus pour ce type de logiciel de se montrer vigilant et de faire prendre conscience aux élèves que l'emploi de la couleur obéit, en matière de cartographie, à des règles aussi rigoureuses que celles définies précédemment ; à savoir s'en tenir, sauf pour des cartes où l'on veut faire apparaître des contrastes, à un dégradé d'une même couleur, allant du plus foncé au plus clair, et ,dans le cas de cartes à comparer, obéir à la règle qui ne tolère aucune exception de la reprise de mêmes couleurs pour représenter des espaces ou des valeurs identiques. Faut-il pour autant, au nom de tout ce qui vient d'être dit, condamner ce type de cartographie qui peut déboucher sur la pire des interprétations ? Ce serait méconnaître la richesse de réflexion qu'elle offre, à condition que l'on joue le jeu et qu'il y ait des séances spécifiques consacrées aux règles à respecter et aux méthodes à suivre. Loin d'être une perte de temps nous y voyons, dans le cadre d'un apprentissage pluridisciplinaire, non seulement un mode d'application concrètes des mathématiques, mais aussi une ouverture sur ce qu'est devenue la cartographie contemporaine dans sa richesse mais aussi ses limites. Claude Loudenot Paru dans la Revue de l'EPI n° 78 de juin 1995. EXEMPLE - 1 - L'AFRIQUE : AFFRIQUE 1990
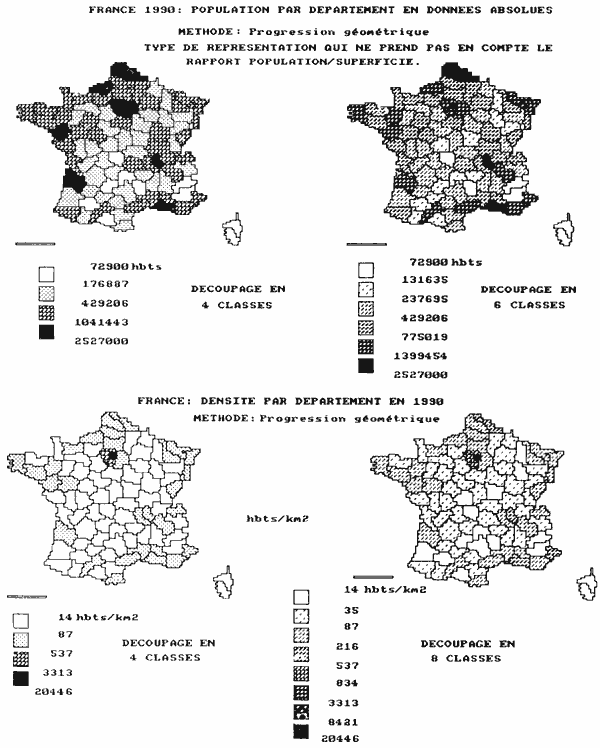
EXEMPLE - 2 - LA POPULATION DE LA FRANCE
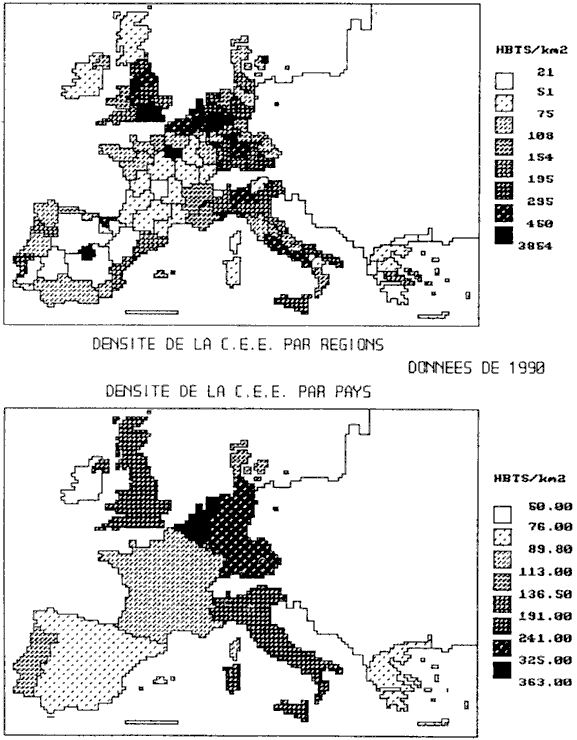
EXEMPLE - 3 - DENSITÉS DES PAYS DE LA CEE PAR RÉGIONS ET PAR ÉTATS
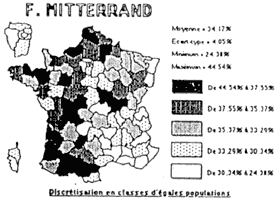
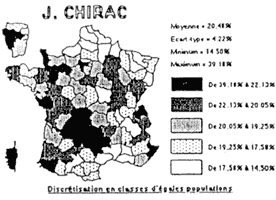
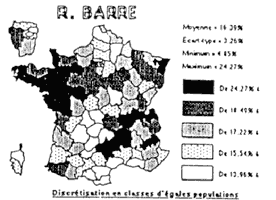
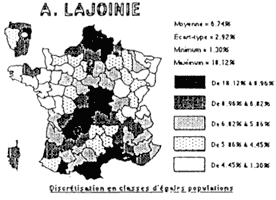
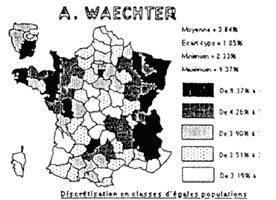
EXEMPLE - 4 - RÉSULTATS DES ÉLECTIONS PRÉSIDENTIELLES DE 1988 Résultats en échelle propre
NOTE [1] C. CAUVIN. « Discrétisation et représentation cartographique » RECLUS Montpellier 1987. ___________________ |