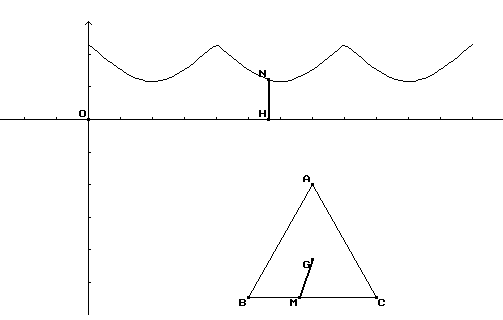
|
Un outil pour illustrer Claudine Voldoire Fin 92, la Direction des Lycées et Collèges adressait à tous les lycées d'enseignement général et technique des imagiciels pour les classes de premières et terminales. Ces imagiciels sont accompagnés d'outils comme le traceur de courbes CARTESI, les générateurs de figures GEOPLAN et GEOSPACE. Au premier abord, je n'ai vu dans GEOPLAN qu'un outil pour la création de figures en géométrie plane (ce qui n'est déjà pas si mal !) que je n'ai pas pu m'empêcher (comme beaucoup de collègues) de comparer au GEOMETRE en regrettant l'ergonomie de celui-ci (création de points libre, déplacement de ceux-ci « à la souris »). GEOPLAN m'a paru faire la part trop importante à l'analytique. (par exemple la première commande du menu point est Point repéré, et la possibilité de création de points quelconques semble marginale). Quand on a ses habitudes, il est difficile d'en changer et il est vrai que l'on risque de perdre beaucoup de temps en papillonnant d'un logiciel à l'autre en quête de performances prétendument nouvelles. La brochure d'accompagnement de GEOPLAN propose la prise en main de celui-ci à travers une activité très riche mais un peu complexe qui risque de décourager si l'on ne dispose pas d'assez de temps pour la mener à son terme. Mes premières approches furent donc peu concluantes. Cependant, la fréquentation des imagiciels, la réussite des activités proposées à partir de ceux-ci, l'insatisfaction due quelquefois à leur côté « fermé », le besoin de les personnaliser, l'envie d'en réaliser de nouveaux et l'inadéquation (eh oui !) des logiciels pratiqués jusqu'alors m'ont conduite à retourner voir du côté de GEOPLAN. Par exemple, la lecture du document INTER-IREM consacré aux modules en seconde (introduction à la notion de fonction et à la notion de fonction périodique) m'a donné envie de compléter le travail proposé par une illustration. Activité 1 (référence IREM : FO03 ) Le point M se déplace sur les côtés d'un triangle équilatéral ABC et on étudie la fonction qui à la longueur de la ligne brisée joignant A à M (en tournant dans le sens contraire des aiguilles d'une montre) associe la distance de M au centre de gravité G du triangle.
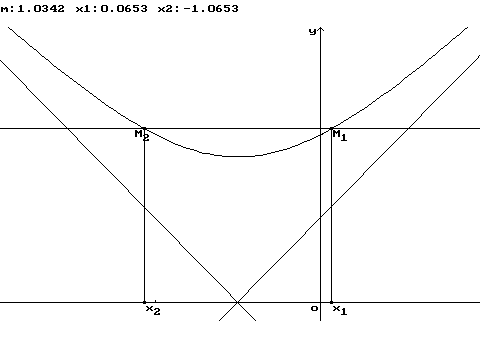
L'activité IREM prévoyait d'expliciter la fonction et de la représenter graphiquement. Il m'a semblé intéressant de compléter ce travail par une observation des déplacements simultanés de M sur ABC et de N sur la courbe. Le paramétrage des côtés du triangle se fait en utilisant la fonction caractéristique m et la seule difficulté rencontrée provient de l'exiguïté de l'espace de saisie des calculs algébriques, ce qui oblige à découper les expressions trop longues. La réalisation de cette figure m'a amenée à utiliser la plupart des fonctionnalités du logiciel et ce fut donc un excellent apprentissage qui a fait naître d'autres idées. J'ai réalisé en particulier que GEOPLAN, avec ses possibilités instantanées d'agrandissement, réduction (touches < et > ) et de déplacement latéral des figures (touches shift+flèches de déplacement) constituait un traceur de courbes très intéressant, offrant bien d'autres possibilités en complément (déplacement d'un point sur la courbe, lecture de coordonnées, de longueurs, de coefficient directeur, d'équation de droite, etc.). J'en ai donc fait un auxiliaire précieux pour l'illustration du cours d'analyse. Dans ma classe de terminale D, j'utilise un poste informatique sur chariot relié à une tablette de rétroprojection pour apporter des illustrations (traceur de courbes, imagiciels sur les suites...). J'ai plusieurs fois été amenée à produire des illustrations avec GEOPLAN parce qu'une présentation traditionnelle n'avait pas donné les résultats escomptés. Par exemple, je n'avais pas pensé que la résolution graphique de f(x) = m soulèverait des difficultés. Je suis donc revenue sur la question en produisant une illustration qui a débloqué la situation, surtout en ce qui concerne le signe des solutions. Activité 2 Suite à l'étude de la fonction définie par Dans l'ensemble, les élèves confondent volontiers nombre de solutions de f(x) = m et nombre de points d'intersection de la courbe C et de la droite d'équation y=m, cependant ils sont peu nombreux à en donner une explication et moins de la moitié d'entre eux est capable de donner le signe des solutions. Devant le faible taux de réussite à cette partie de la question, j'ai donc proposé l'image suivante, avec une droite d'équation y = m (m étant une variable réelle mobile).
Notons la possibilité d'obtenir l'affichage de valeurs approchées de m et des solutions x1 et x2 de l'équation (lorsqu'elles existent). Signalons cependant que l'on ne peut définir directement les points d'intersection d'une courbe quelconque et d'une droite, d'où le recours à un subterfuge en définissant x1 et x2 comme les images de m quand elles existent par chacune des fonctions réciproques de f sur les intervalles Activité 3 L'inégalité des accroissements finis se révèle un des résultats les plus difficiles à bien interpréter et encore plus à appliquer (encore que simple à démontrer) Énoncé : Si f fonction dérivable sur un intervalle I et telle que sa fonction dérivée soit bornée sur I (m < f'(x) < M) alors, pour deux éléments quelconques a et b de I tels que a < b on a :
Chaque choix arbitraire de a conduit à un encadrement de f(b) ; cela revient à encadrer la fonction f par des fonctions affines de coefficients m et M, et dont la représentation contient le point A(a, f(a)). On se trouve donc en présence d'une infinité d'inégalités doubles, parmi lesquelles il faut faire un choix (en particulier dans les exercices où l'on utilise le théorème pour rechercher une valeur approchée de f(b)). J'ai essayé d'en donner une illustration.
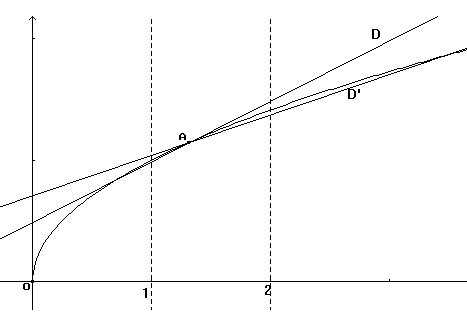
Description de l'activité avec la classe : Représenter graphiquement la fonction f définie sur R+ par : f(x) = Choisir un point A de la courbe dont l'abscisse a est variable dans l'intervalle [1 ; 2]. Tracer les droites D et D' passant par A et de coefficients directeurs respectifs 1/2 et 1/3. Choisir le mode « MOBILE » et faire varier a dans [1 ; 2]. On observe que la partie de la courbe correspondant à l'intervalle [1 ; 2] reste dans le secteur angulaire délimité par les deux droites D et D'. Écrire les inégalités traduisant cette situation :
Modifier la définition de la variable a pour la faire varier dans [0 ; 3] et observer que la propriété précédente n'est plus vraie. Observer les variations de la fonction dérivée de f sur [1 ; 2] et encadrer f' sur cet intervalle. Énoncer et démontrer le théorème général. Il s'agit de bien faire comprendre que sur l'intervalle [1 ; 2], la courbe se trouve dans le secteur angulaire de sommet variable défini par les droites D et D'. Mes activités de formateur MAFPEN m'ont amenée à rencontrer de nombreux collègues intéressés par les imagiciels, mais qui n'ont pas eu le temps de s'intéresser à GEOPLAN ou qu'une première approche n'a pas convaincu. En construisant devant eux et avec eux une application simple, il m'a semblé que la facilité d'exécution, la richesse des commandes(*) et la qualité des réalisations réussissaient à vaincre bien des scepticismes. Ceux qui cherchent le moyen de réaliser rapidement des images adaptées à leurs préoccupations immédiates devraient s'approprier cet outil efficace et dont la diffusion mériterait d'être étendue à tous les collèges et lycées professionnels avec peut-être une adaptation des menus afin de les débarrasser des commandes non pertinentes (exemple : mesures en radians, produit scalaire, barycentre pour les collèges)(**). Claudine Voldoire Paru dans la Revue de l'EPI n° 76 de décembre 1994. (*) Pour en donner un aperçu, le menu points suivi de transformés donne accès à
et rotation vous propose
Que souhaiter de plus ? Bien sûr, les virtuoses des macro-constructions seront déçus, mais pourquoi faire compliqué... (**) Cette adaptation est maintenant possible dans la version 2 diffusée par le CRDP de Poitiers. ___________________ |
et au tracé de sa représentation graphique C, on se propose de discuter graphiquement, selon les valeurs de m, le nombre et le signe des solutions de l'équation f(x) = m.
; -0.5]
.
