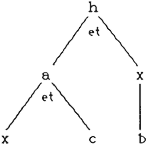
Un exemple d'apport de l'informatique à la biologie
(1^ère partie)

Alain Langouet
 

INTRODUCTION : Certaines situations expérimentales particulièrement riches, qui sont en général peu ou pas abordées par l'enseignement, nécessitent, de la part des élèves, la mise en oeuvre de raisonnements complexes. On leur demande de se « mettre dans la peau » des chercheurs qui ont conçu celles-ci et cela n'est pas sans leur poser de nombreux problèmes. Dans une première partie, nous évoquerons plus particulièrement ceux relatifs à quelques utilisations de l'informatique dans l'enseignement secondaire de la biologie. Nous essayerons ensuite de montrer ce que nous semble pouvoir apporter l'intelligence artificielle (I.A) aux logiciels destinés à l'enseignement et à l'apprentissage. Dans une seconde partie, à travers un exemple concret qu'il nous a été donné d'approfondir dans le cadre d'une recherche menée à l'INRP [1], une tentative d'application des concepts et méthodes de l'I.A à un type de raisonnement en biologie sera présentée. Une discussion des implications didactiques de la modélisation des raisonnements sera enfin présentée.

A. ANALYSE DE QUELQUES ASPECTS DE L'UTILISATION DE L'INFORMATIQUE DANS L'ENSEIGNEMENT SECONDAIRE DE LA BIOLOGIE.

1. Intérêts, rôles et limites de certains logiciels dans l'enseignement expérimental de la biologie.

     On peut dresser une typologie des logiciels selon différentes approches : le mode d'interaction avec l'apprenant, la théorie de l'apprentissage sous-jacente, le type d'activité cognitive sollicité...

     Si l'on observe, par exemple, le mode de relation avec l'apprenant. Il peut y avoir des interactions très orientées dans ce que l'on appelait des tutoriels ou, maintenant, dans des environnements guidés d'apprentissage [2]. On peut, au contraire, avoir des logiciels de découverte très libres laissant toute latitude au professeur pour les insérer dans leur progression pédagogique. Sont-ils utilisés ? Des didacticiels mettent en oeuvre une ou plusieurs conceptions ou théories de l'apprentissage. Est-elle ou sont-elles explicitées ?

     Un certain nombre de catégories [3] de logiciels, dont la typologie est très informatique, peut être distingué en biologie : banques de données, épidémiologiques ou moléculaires par exemple, simulations, logiciels de traitement d'images satellitaires, logiciels de modélisation, des zones de subduction par exemple, logiciels professionnels [4]. De même qu'il est envisageable, mais non évident, de faire une transposition didactique d'outils professionnels tels que le traitement de texte en bureautique [5], des chercheurs [6] se penchent sur l'utilisation de logiciels professionnels en biologie et en géologie.

     Nous constatons, cependant, les réticences des enseignants et même des élèves devant les difficultés d'utilisation de logiciels, souvent de plus en plus complexes. Pour pouvoir les utiliser, il faut sans doute prévoir d'en faire de solides transpositions didactiques. Les pays anglo-saxons ont élaboré de nombreux logiciels de biologie, ils ressemblent un peu aux nôtres, des échanges seraient, à cet égard, sans doute fructueux. Une typologie de leurs utilisations est révélatrice des mêmes interrogations mais aussi de nuances  [7]. Ils proposent, par exemple, des activités de modélisation informatique de concepts dynamiques de relation et de transfert de matière et d'énergie entre êtres vivants dans un écosystème [8] alors que n'avons à notre disposition que des simulations dans ce domaine.

     Les logiciels et, plus généralement, les activités de simulation présentent des intérêts spécifiques sur le plan cognitif. J. Hebenstreit [9] souligne que la simulation permet de se situer à un niveau d'abstraction intermédiaire entre le réel et le modèle abstrait (ou la théorie). C'est, en soi, une position originale qui a des avantages pédagogiques peu explorés. La simulation [10] fait peut-être peur, ne serait-ce que par ses connotations trompeuses. On lui fait de nombreux reproches tous plus injustifiés les uns que les autres, car aucun ne semble s'appuyer sur des arguments sérieux ou établis.

     Si l'on situe la spécificité des activités qui peuvent être envisagées avec une simulation informatique, d'un phénomène biologique, tout change. Mais il faut poser les problèmes en terme de comparaison entre avantages et inconvénients. Il ne faut pas se leurrer avec des outils technologiques chargés de tous les bienfaits de la terre. Parmi les arguments d'ordre psychologique et psycho-cognitif on peut citer le caractère motivant mais aussi très déroutant de la simulation, si elle est libre. On peut, éventuellement, comparer avec la consultation d'un document hypermédia, qui a de quoi égarer plus d'un « navigateur » ! Mais à cette dernière, s'ajoute le caractère dynamique des résultats fournis par la simulation.

     Les avantages ont été décrits à travers de nombreux exemples [11] comme la rapidité d'accès aux résultats, le fait de pouvoir se concentrer sur le raisonnement, d'avoir accès à des manipulations dangereuses, fastidieuses, longues ou onéreuses... et donc de s'affranchir d'un certain nombre de contraintes. Faut-il que les logiciels de simulation disposent de moyens d'évaluation [12], au-delà de la note chiffrée, gadget pédagogique, au demeurant fort stimulant. Est-ce tout ce que l'on peut proposer comme remarques aux élèves ? Il faut dépasser les arguments stériles opposant logiciels dirigés et environnements libres, certains des premiers, dont les objectifs ont été clairement définis, sont plus efficaces que certains des seconds [13]. Le problème est de savoir quel obstacle ils se proposent de faire franchir, quel objectif de savoir ou de méthode ils se proposent de faire atteindre.

     On a aussi reproché aux logiciels de simulation, et plus généralement à l'informatique pédagogique, de supprimer les activités expérimentales, de nombreux arguments montrent le contraire [14]. « La simulation ne remplace rien ; c'est un outil nouveau », complémentaire « qui permet des types d'activité pédagogique qui n'étaient pas possibles jusqu'à présent et peuvent améliorer les processus d'apprentissage » [15].

     Soulignons enfin le besoin de synthèse entre des réalisations parfois similaires dans différentes académies, régions et même pays.

     Pouvons-nous utiliser des outils informatiques pour passer de simulations relativement brutes à des simulations qui permettent d'entraîner à la démarche expérimentale, de modéliser les phénomènes découverts, d'évaluer les productions de l'élève... Pour lever un certain nombre de difficultés, et élargir les compétences de ces logiciels, il semble que les techniques et les idées développées par l'intelligence artificielle soient à considérer.

     Mais, avant cela, nous voudrions évoquer les problèmes posés par l'utilisation de ces logiciels en biologie.

2. Les problèmes posés par la conception et l'utilisation de logiciels de simulation.

     G.L Baron explique et rappelle [16] que les logiciels ont historiquement débuté par une approche de type béhavioriste (modèle stimulus-réponse) avec l'enseignement programmé puis l'EAO [17], qui est aujourd'hui partiellement délaissé. Puis sous l'impulsion de S. Papert, au MIT  [18], et d'autres chercheurs, se sont développés les micro-mondes, environnements libres dans lesquels les élèves sont en mode « commande ». Un consensus semble s'établir autour du fait que ces environnements ne garantissent pas, pour motivants qu'ils soient, des apprentissages efficaces. Ils n'en sont pas, pour autant, nécessairement, des outils inutiles. Certains chercheurs essaient alors de les coupler avec des modules « tutoriels intelligents » [19].

     Ces logiciels dédiés sont longs à produire et leur efficacité n'est pas assurée. Nous manquons d'études pour les évaluer. Les logiciels actuels sont peu satisfaisants, sur de nombreux points, mais les doter de tutoriels intelligents prend du temps, nécessite le travail d'équipes pluridisciplinaires de didacticiens, informaticiens, psychologues...

     De nombreux autres problèmes viennent se greffer sur ceux-ci. Le choix des sujets à informatiser, la modélisation de ceux-ci selon le niveau du public, qui ne doit être ni trop simple ni trop complexe. Le problème de la formation à ces nouveaux outils qui ne font pas partie des traditions du corps enseignant.

     La gestion des interactions élève-machine, mais aussi enseignant-élève, qui est tout à fait particulière, pose des problèmes de pédagogie extrêmement différenciée. Dans la mesure où les situations abordées sont plus complexes, il importe de mieux s'y préparer, la complexité et l'abondance des données pose le problème de leur traitement. Il y a nécessité d'introduire et de diversifier les démarches scientifiques. L'informatique pousse au progrès, elle génère les problèmes, en même temps que les solutions pour les surmonter, en une spirale récurrente.

     Devant ces faits, ayant nous-même utilisé des logiciels, en biologie, au lycée et au collège, et pratiqué l'enseignement de l'informatique au lycée, nous avons voulu nous poser le problème de la formation et du suivi du raisonnement des élèves.

     Comment saisir le comportement des élèves, suivre leur raisonnement, leur apporter des aides efficaces, lesquelles et quand ? Comment peuvent-ils vaincre leurs difficultés en situation de résolution de problèmes ? Quelles stratégies, hypothèses, logiques développent-ils ? Comment les confronter aux démarches des scientifiques ? Quel(s) modèle(s) de raisonnement du chercheur en biologie sommes nous capables de leur présenter ? Quelles sont les réponses de l'informatique devant ses problèmes ? Quels sont ses intérêts et ses limites ?

     Et tout d'abord, puisque l'intelligence artificielle a permis de réunir des disciplines aussi diverses que la psychologie, l'informatique, la linguistique et les neuro-sciences... Quels sont les apports spécifiques de celle-ci pour la formation et la compréhension des raisonnements des élèves en sciences expérimentales ?

B. QUELS SONT LES MOYENS INFORMATIQUES DE MODÉLISATION DU RAISONNEMENT

     Nous présentons succinctement un des langages de l'intelligence artificielle : Prolog, le concept de système expert qui a fait ses preuves en Médecine et en Géologie par exemple ainsi que les interactions fructueuses qui peuvent en résulter.

1. Un langage de (pour) l'intelligence artificielle : Prolog

     Nous aborderons ici un certain nombre d'aspects de ce langage qui offre des possibilités très intéressantes. Prolog a de multiples facettes, il peut être considéré comme un gestionnaire de bases de données relationnelles très interactif, agréable à utiliser, mais aussi comme un langage favorisant la mise au point de maquettes de logiciels. La façon d'énoncer les connaissances, « en vrac », en fait un langage déclaratif qu'on oppose aux langages impératifs où les ordres donnés apparaissent de façon explicite dans le texte du programme. Mais il est néanmoins très utile de savoir comment Prolog fonctionne afin de tirer partie de toutes ses potentialités et d'éviter certains de ses défauts. Ceci impose la connaissance du fonctionnement du moteur d'inférences de Prolog. Ce « moteur » fait que l'on qualifie parfois Prolog de démonstrateur automatique de théorèmes, il faut entendre par là les théorèmes de la logique formelle du premier ordre.

     Il est possible d'aborder ce langage très puissant de façon intuitive et cela contribue à lui donner un aspect particulier que n'ont pas d'autres langages. Il est même utilisé à des fins d'initiation à l'informatique.

     Dans un de ses livres [20] J.L. Laurière explique le principe de résolution qui est intégré au langage Prolog. Il est basé, entre autres, sur le théorème d'Herbrand. Celui-ci postule que pour démontrer le théorème T soit H1 & H2 & ... & Hn => C, où H1 & H2...et C (ex : site de culture = sang & organisme gram négatif & organisme de forme bâtonnet & patient = hôte à risque => probabilité que l'organisme soit Pseudomonas aeruginosa = 0.6 [21]) sont des formules de la logique des prédicats [22] et => le symbole de l'implication, il peut être plus facile de démontrer que la formule F : H1 & H2 & ... & Hn & ~C est contradictoire (avec les données du problème ; les symptômes présumés d'une pathologie par exemple) en utilisant alors un raisonnement par l'absurde [23].

     Il suffit alors de trouver un contre-exemple pour la formule F. On voit ici l'analogie avec le raisonnement hypothético-déductif qui peut effectivement aboutir à une contradiction entre hypothèses et résultats expérimentaux et conduire ainsi à rejeter ou infirmer l'hypothèse  [24]. La différence est qu'il s'agit dans l'exemple ci-dessus de rejeter la négation du théorème et non le théorème lui-même.

     La contradiction va toujours être atteinte en un nombre fini d'étapes, quelles que soient les valeurs de vérité données aux fonctions qui interviennent dans les hypothèses et la conclusion. Le théorème d'Herbrand (1930) [25] indique : « une condition nécessaire et suffisante pour qu'un ensemble E de clauses soit inconsistant (ou contradictoire) est qu'il existe un ensemble fini contradictoire de sous-formules de E complètement instanciées » [26].

     L'unification est le mécanisme par lequel sera recherchée la valeur des variables permettant d'aboutir à la contradiction recherchée.

     Soit un théorème T[27] : H (hypothèses) => C (conclusion) (par exemple homme(X) => mortel(X)) et une expression E (homme(socrate)). Il s'agit de voir s'il est possible de rendre H et E complètement identiques (X=socrate), c'est-à-dire d'unifier H et E par une suite de substitutions de variables libres [28] dans H et E. Si cela est possible, ces substitutions effectuées dans C (mortel(socrate)) donnent la nouvelle forme de l'expression E (mortel(socrate)) après application (ou déduction) du théorème T, par utilisation du modus ponens. Cette méthode de démonstration est qualifiée de puissante car elle est systématique. Elle est aussi élégante. Néanmoins on ne peut démontrer que des théorèmes avec cette méthode. On ne peut trouver ou inventer de conjectures. Si la proposition n'est pas un théorème, la résolution peut ne jamais se terminer !

     L'interprèteur de Prolog (il en existe de nombreuses versions) est basé sur le principe de résolution de Herbrand (1931) repris et programmé par J.A. Robinson (1965) qui systématise le raisonnement par l'absurde. Pour démontrer p => q, il démontre que p & ~q est contradictoire. La représentation des faits et des règles est uniforme. Son efficacité est bonne. Prolog offre l'accès à l'arbre de preuves [29], au mécanisme de retour-arrière ou backtrack qui permet de revenir sur les (noeuds) OU de l'arbre de preuves afin de tenter de démontrer le but d'une nouvelle façon. On peut, de plus, écrire en Prolog les mécanismes de contrôle d'exécution des processus de déduction grâce à des prédicats d'ordre deux [30]. Les clauses de Horn, par exemple C1 & C2 & ... & Cn & ~P  [31], qu'utilise Prolog sont très proches des règles de production du type si C1 & C2 & ... & Cn alors P.

     Prolog a l'avantage de bénéficier d'un algorithme d'unification tout fait, d'un mécanisme de gestion de l'arbre de recherche ET-OU. Il fait quatre types d'inférences sous une seule forme [32] à partir de p => q :

2. Notion de système expert, de moteur d'inférences

     Un système expert est principalement composé des éléments suivants [33] : la base de connaissances, l'interface entre celle-ci et l'expert, le moteur d'inférences qui fait le lien entre la base de faits et la base de connaissances, l'interface avec l'utilisateur.

     Le moteur d'inférences ou moteur de résolution est le coeur du système expert, il peut être indépendant du domaine d'application, c'est lui qui contient tous les algorithmes d'exploitation des connaissances ou de résolution de problèmes.

     Les interfaces permettent la communication avec les utilisateurs. On voit ici qu'ils sont de deux types : les interfaces seront probablement différentes car un expert peut être utilisateur mais ne l'est pas forcément, tandis qu'un utilisateur standard n'est pas expert, en général.

     La base de connaissances est souvent constituée de règles de production de la forme « si ... alors ... » décrivant les relations pouvant exister entre certains faits ou certaines actions à exécuter dans des circonstances particulières.

     Par exemple : si la teneur en ions Na+ du milieu intérieur augmente alors il y a augmentation de la sécrétion de rénine. Ou bien si l'hypothèse est d'infirmer une éventuelle « hérédité liée au sexe » d'un caractère récessif alors chercher s'il existe, dans la généalogie, un couple dont la (une) fille est porteuse du caractère et dont le père ne l'est pas.

     La base de faits contient des connaissances élémentaires et s'enrichit au fur et à mesure de faits déduits par le moteur d'inférences.

3. Modes de fonctionnement du moteur d'inférences (M.I) : marche arrière, marche avant [34]

     Pour mieux apprécier le fonctionnement d'un système expert prenons un exemple [35] : soit la base de connaissances suivante, constituée d'un certain nombre de règles de production (arbitraires) numérotées.

     Soit la base de faits connus : b, c. (seuls les faits b et c sont connus au départ)

     Soit le but h c'est-à-dire démontrer h. En marche arrière [36] le moteur d'inférences cherche à démontrer le but en combinant les faits de la base de faits avec les connaissances de la base de connaissances. En profondeur, il explore à fond les sous-buts (a et x) rencontrés en déclenchant les règles qui ont pour conséquent h (ici R6) [37], puis les sous-sous-buts (d, g...)... au fur et à mesure qu'ils sont rencontrés.

     Le mécanisme de marche arrière est déjà intégré au langage Prolog. Celui-ci fonctionne tant que la liste de sous-buts n'est pas vide, c'est-à-dire tant que des règles sont encore applicables. Lorsque le processus s'arrête, soit le but est un fait ou la liste de sous-buts est une liste de faits (donc présents dans la base de faits, ici pour nous b et c) et le but est alors démontré, soit l'un, au moins, des sous-buts ne correspond à aucun des faits présents et il y alors échec.

     Mais en cas d'échec, soit on se situe dans l'hypothèse du « monde clos » et c'est terminé, soit on peut ouvrir vers l'extérieur et convenir que le M.I demande par exemple à l'utilisateur si le fait (ou les faits) manquant(s) est (sont) « vrai(s) », présent(s), vérifié(s)... [38] Le système peut, par exemple, solliciter du médecin un certain nombre d'informations sur un patient. Un exemple d'information requise par le système lors du déclenchement d'une règle pourrait être : s'il y a une suspicion de telle pathologie, alors demander tel paramètre, ou, s'il n'est pas connu, le résultat de telle analyse...

     C'est le moteur d'inférences de Prolog [39] qui va lancer la résolution du but h lorsqu'on lui en exprimera la requête, il utilise pour cela un processus en marche arrière, en profondeur. Il s'agit d'un raisonnement régressif (ou rétrospectif) qui utilise des conditions nécessaires.

     Démontrer le but h revient donc à exprimer la requête suivante au M.I de Prolog : h ? où le « ? » est le symbole de cette requête.

     Si l'on souhaite que Prolog s'arrête dès qu'une première solution dans l'arborescence de preuves a été trouvée, il faut adjoindre à la requête un « cut » dont le symbole est le caractère « ! ». Celui-ci a une fonction de coupe-choix c'est-à-dire d'élagueur des points de choix représentés par les noeuds « ou » de l'arbre de preuves. La requête devient ainsi h,! ? ce qui peut se lire : peut-on démontrer le but h et (symbole « , ») si oui s'arrêter en donnant la première solution trouvée ?

     Voici un exemple de « moteur » très simple fonctionnant en marche avant  [40], il engendre un arbre de preuves assez important puisqu'il fonctionne dans « tous les azimuts » et ne cherche pas, comme dans la requête précédente, à ne démontrer qu'un seul but. Il fait des inférences déductives. Il s'agit d'un raisonnement prospectif qui utilise des conditions suffisantes.

     Les seules règles dans la base sont, en l'état (R1) qui vise à démontrer le but f, (R2)... [41]

     Avant de lancer le but déduire, c'est-à-dire d'essayer de résoudre la liste des buts [f,a,x,e,h,d], la base de faits était réduite aux deux faits b et c. Après l'exécution, à celle-ci s'ajoutent les faits déduits a, d, e, f, h.

Alain Langouet

Suite de l'article dans le n° 73 de la Revue de l'EPI.

Paru dans la  Revue de l'EPI  n° 72 de décembre 1993.
Vous pouvez télécharger cet article au format .pdf (302 Ko).

NOTES

[1] Langouet A. Intelligence Artificielle et formation à la démarche expérimentale et au raisonnement en biologie, Mémoire de DEA de Didactique des Disciplines, Université Paris VII, 166 p. + annexes, 3.7.1992.

[2] (NIC & al.88) Nicaud J.-F., Vivet M. Les tuteurs intelligents : réalisations et tendances de recherches. T.S.I. Vol. n°7, n°1 numéro spécial, 1988.
(VIV90) Vivet M. Apports de l'intelligence artificielle. in Informatique et apprentissages. Actes de l'université d'été de Châtenay-Malabry, Université Paris Sorbonne, CNRS - GDR 957, INRP, p. 131-142, 1990.

[3] (JER79) Jérome P. L'informatique, support logique de la démarche expérimentale. Buletin de l'APBG, n° 4, Paris, 1979.

[4] (SAL & al.89) Beaufils D., Salamé N. « Quelles activités expérimentales avec les ordinateurs dans l'enseignement des Sciences ? », ASTER, recherche en didactique des Sciences Expérimentales, n°8, INRP, département de didactique, 55-79, 1989.

[5] (LEV91) Levy J.-F. Le traitement de texte en formation professionnelle de niveau V et III. Observations et questions. in Informatique et apprentissages, Actes de l'université d'été de Châtenay Malabry, INRP, Paris, p. 107-128, 1991.

[6] (BEA & al.90) Beaufils D., Salamé N. Informatique et enseignement : étude de cas, in Informatique et apprentissages. Actes de l'université d'été de Châtenay-Malabry, Université Paris Sorbonne, CNRS - GDR 957, INRP, 1990.
(SAL89) Salamé N. Potentialités actuelles de l'informatique dans l'enseignement de la biologie et de la géologie. In L'ordinateur en classe de biologie-géologie, CARFI, Versailles, p. 5-16, 1989.

[7] (TAL83) Tallon B., Tomley D. & Derek B. Microcomputers and biology teaching - an overview and some ideas for future development. in The school science review, vol. n°65, n°231, décembre 1983.

[8] (TAL83) Ibid. p. 260-263.

[9] (HEB88) Hebenstreit J. Simulation et pédagogie. Une rencontre du troisième type. AFCET/INTERFACES n°65 14-18, mars 1988.

[10] Selon l'Encyclopédie Universalis la simulation est l'expérimentation sur un modèle, mais la simulation est aussi la dissimulation d'un contrat secret, la feinte d'une maladie pour en tirer avantage... (Gd. Larousse universel)

[11] (LES88) Lestournelle R. « Simulation en biologie », p. 119-124, Bulletin EPI n° 49, mars 1988. (voir aussi répertoire informatisé PC/MS-DOS des articles EPI parus de 1971 à 1993).

[12] C'est notre avis ainsi que celui de Lestournelle R. (LES88) op. cit. p. 122.

[13] De nombreux exemples de logiciels de ce type ont été produits par des équipes de biologistes de l'université Paris VII (Jussieu) en embryologie, biologie cellulaire, et de l'université d'Orsay en génétique...

[14] (SAL & al.89) op. cit.

[15] (HEB88) op. cit. p. 16. Voir aussi « L'intégration de l'informatique dans l'enseignement et la formation des enseignants », coédition INRP-EPI, 284 pages, 1992.

[16] (Hypermédias..91) Collectif. Hypermédias et Apprentissages. Actes des premières journées scientifiques, édités par B. de La Passardière et G.-L.Baron, 24-25 Sept. 1991.

[17] Enseignement Assisté par Ordinateur.

[18] Massachussets Institute of Technology.

[19] (Hypermédias. 91) op. cit. p.8.

[20] (LAU86) Laurière J.-L. Résolution de problèmes par l'homme et la machine, Paris, Eyrolles, 1986.

[21] (COR84) op. cit. Il s'agit d'un exemple de règle ou « théorème » extrait du premier système expert médical crée Mycin.

[22] Ce sont des fonctions logiques utilisant des variables dont le résultat est vrai ou faux.

[23] ~C signifie non C.

[24] (DUP92) Dupont M. Quelques problèmes posés par l'évaluation des raisonnements en sciences chez l'élève, in Aster n°15 Lumières sur les végétaux verts. 1992.

[25] (LAU86) op. cit. p.132.

[26] C'est-à-dire dont les variables ont pris des valeurs précises qui rendent les sous-formules contradictoires. (exemple : p & ~p ; ou & est le et logique, ~ le non logique).

[27] (LAU86) op. cit. p.92.

[28] N'ayant aucune valeur prédéfinie.

[29] C'est à dire la trace du (des) raisonnement(s) effectué(s) par le moteur d'inférences (voir aussi § 3.)

[30] Ce sont des méta-prédicats qui utilisent des paramètres qui sont des prédicats d'ordre un.

[31] Conjonction (et logique) de formules logiques dont une seule est "négative", ici la dernière (~P) soit : C1 & C2 & ... & Cn & ~P.

[32] (LAU86) op. cit. p. 354.

[33] (COR84) Cordier M.O. Les systèmes experts. in La Recherche, n° 151, vol. 15, p. 60-70, janv. 1984.

[34] Le terme chaînage est hérité des pays anglophones (chaining), "marche" est le terme équivalent français.

[35] (COR84) Ibid. p.64.

[36] La marche arrière est un des modes de fonctionnement d'un moteur d'inférences.

[37] Dans l'implication p => q (si p alors q) q est le conséquent, p est l'antécédent.

[38] Voir, comme exemple d'interrogation de l'utilisateur par un système expert, l'interrogation de sphinx, système expert réalisé à la faculté de médecine de Marseille, spécialisé dans le diagnostic des ictères (« jaunisses » et présence de pigments biliaires dans les tissus), « Y a-t-il une notion de colique hépatique ? ». (COR84) op. cit. p.62.

[39] Il s'agit d'un M.I. d'ordre un, c'est-à-dire utilisant des variables et relevant de la logique des prédicats (les prédicats sont des fonctions logiques utilisant des variables dont les valeurs sont vrai et faux). Dans cet exemple il n'y a pas de variables, on pourrait donc utiliser un M.I. d'ordre zéro n'utilisant que des événements vrais ou faux, présents ou absents, relevant de la logique des propositions.

[40] C'est-à-dire en essayant de démontrer tous les buts possibles dans la base de connaissances (base de règles) et enrichissant au fur et à mesure la base de faits déduits (inférence déductive).

[41] On pourrait par exemple permettre à un utilisateur donné d'ajouter de nouvelles règles...

___________________
Association EPI

Sommaires des Revues