MODELSCREATOR
Un logiciel de modélisation permettant l'utilisation des règles logiques et la prise de décision

Panagiotis POLITIS, Vassilis KOMIS,
Angélique DIMITRACOPOULOU
 

     Les processus de résolution de problèmes et de prise de décision constituent une question importante de l'enseignement et de l'apprentissage. Les compétences acquises par les élèves au cours de ces processus devraient se trouver au centre même de l'acte éducatif. Cet article traite des processus de prise de décision dans le cadre de résolution des problèmes à l'aide du logiciel éducatif ModelsCreator. Ce logiciel constitue un environnement ouvert d'apprentissage, permettant aux élèves de concevoir, de construire et de modifier des modèles. Il s'agit d'un environnement de modélisation mettant l'accent sur le raisonnement qualitatif et semi-quantitatif, ainsi que sur les moyens alternatifs d'expression et de visualisation des modèles. Nous étudions les aspects de construction des modèles d'ordre logique et de prise de décision, de l'étude de leur comportement et de leur amélioration.

INTRODUCTION

1.1. À propos de la notion de modélisation

     La modélisation, composant essentiel de l'activité humaine, se représente du moment où l'homme essaye de comprendre et d'interpréter les divers phénomènes du monde et de faire des prévisions. Un modèle, comme une représentation formelle d'un problème, d'un processus, d'une idée ou d'un système n'est jamais une réplique exacte, mais plutôt une image stylisée et abstraite et il a comme but de représenter les aspects essentiels de la structure, des propriétés ou du comportement de ce dont il est le représentant. En décrivant le processus de modélisation, nous pouvons distinguer six étapes importantes (Webb, 1993) :

1. Précision et définition du problème ou du système à modéliser.

2. Définition du but du modèle.

3. Décision sur les aspects principaux du modèle.

4. Définition des relations entre les composantes du modèle.

5. Évaluation du modèle avec contrôle de son comportement par rapport à ses objectifs.

6. Répétition de ce processus au moins de l'étape trois, s'il est nécessaire.

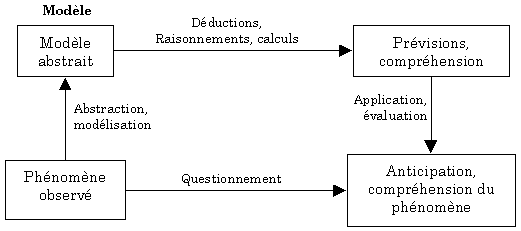
     Un modèle, selon Ferber (1995), sert à la prévision et à la compréhension des phénomènes et le processus de modélisation peut se représenter tel le schéma suivant (schéma 1).

Schéma 1 : Prévision et compréhension par le processus de modélisation

     Il est à noter que ces dernières années, la "façon de fonctionnement" de certaines sciences (physique, mathématiques, géologie, biologie, astronomie, etc.) a été profondément modifiée grâce aux possibilités de processus de modélisation que les ordinateurs permettent. Les logiciels de modélisation constituent une catégorie particulière dans le cadre du développement des applications informatiques et peuvent être considérés comme la suite de la notion des micromondes (Papert, 1980) : fournir aux usagers des outils de traitement et d'apprentissage par l'expression et par l'exploration. Ils s'avèrent par conséquent très utiles pour la recherche scientifique, l'éducation et la formation. Un système de modélisation, grâce à son caractère ouvert, permet de mener des activités diversifiées, mais il suppose des efforts particuliers concernant sa réalisation. L'usager du système peut construire ses modèles au moyen d'un processus actif et personnalisé. Dans ce sens, les activités de modélisation - s'inscrivant dans une tradition constructiviste - sont susceptibles d'aider de façon significative les apprentissages.

1.2. Les logiciels éducatifs de modélisation

     Les étapes de modélisation dans un environnement informatique ne sont pas différentes de celles décrites auparavant. Pourtant, à la différence des modèles non computationnels, un modèle sur ordinateur est "exécutable", muni donc d'une dynamique qui n'existe pas dans les autres modèles. En même temps, la création d'un modèle dans un environnement informatique permet de le dessiner très facilement, de le voir évoluer et surtout de le simuler.

     Nous pouvons classer en trois catégories les logiciels de modélisation : modélisation quantitative, modélisation qualitative et modélisation semi-quantitative.

     I. Logiciels de modélisation quantitative. Le modèle quantitatif fonctionne sur des grandeurs mesurables et les relations régissant entre les grandeurs sont exprimées par des formules algébriques. Nous sommes en mesure de créer ou d'explorer des modèles de tel type. La quasi totalité des logiciels de modélisation appartiennent à cette catégorie, comme les tableurs etc.

     II. Logiciels de modélisation qualitative. Les modèles qualitatifs expriment les connaissances qui ne peuvent pas être exprimées de façon mesurable. Ce sont des connaissances dont les bornes de validité ne se dessinent pas clairement, mais elles constituent néanmoins une grande partie de ce programmes scolaires. Dans cette catégorie, nous pouvons classifier certains systèmes experts, les logiciels de cartes conceptuelles, les jeux d'aventure, etc.

     III. Logiciels de modélisation semi-quantitative. Les modèles semi-quantitatifs ne se basent pas forcement sur des grandeurs mesurables et ils n'expriment pas la valeur, mais l'influence d'une partie d'un système sur une autre partie (Bliss et al., 1992 ; Mellar et al., 1994). Ils concernent donc des modèles qui fonctionnent de façon pratiquement qualitative. Le raisonnement dans ces systèmes porte sur des grandeurs dont nous cherchons en principe le signe et non la valeur (Bruillard, 1996).

     Les logiciels de modélisation, qui sont des systèmes ouverts, permettent plusieurs types d'activités et leurs usages peuvent se représenter en deux axes (table 1) (Bliss et al., 1992) :

• expression (activités de modélisation, au moyen de la création de nouveaux modèles) ;

• exploration (activités d'exploration de modèles existants, au moyen de leur simulation).

     Les activités d'expression offrent aux apprenants la possibilité de dégager les paramètres actifs pour décrire à l'aide d'un modèle, le comportement d'un système (démarche ascendante : la recherche des lois à partir de l'expérience), tandis que les activités d'exploration leur fournissent la possibilité de valider des hypothèses de comportements prédits à partir de l'observation préalable (démarche hypothético-déductive).

Table 1 : Catégories générales des types et des usages de modélisation.

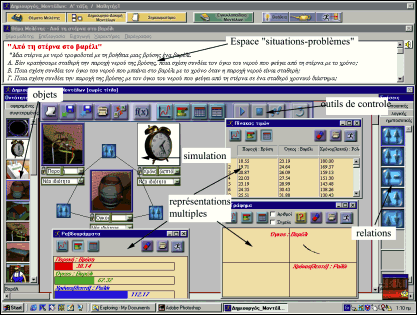
     Certains des systèmes existants supportent des modèles dynamiques comme MODELLUS (Teodoro 1997), approprié pour la modélisation quantitative mathématique, ou STELLA (http://www.hps-inc.com). Il y a deux systèmes qui supportent le raisonnement semi-quantitatif, IQON (Bliss et al., 1992) et Model-It (Soloway et al., 1996). Expert Builder (Webb 1993) supporte des modèles qualitatifs de logique, tandis que AXON et INSPIRATION (http://www.inspiration.com) permettent la construction des cartes conceptuelles. Certains de ces systèmes ne sont pas appropriés pour les jeunes enfants (p.e. STELLA et MODELLUS) ayant des interfaces complexes et surtout des représentations assez abstraites, tandis que d'autres supportent un seul type de modèles (dynamique, de carte conceptuelle ou logique) et ils sont focalisés dans des domaines d'étude spécifiques. C'est pourquoi nous avons conçu et développé un nouvel environnement de modélisation permettant aux jeunes élèves (11-15 ans) de mener des activités de modélisation, appelé ModelsCreator. C'est un environnement ouvert permettant de travailler sur des entités (représentant des objets) et sur leurs propriétés (représentant des concepts) liées par des relations d'ordre qualitatif (des liens logiques), semi-quantitatif (expression qualitative des formules mathématiques) ou quantitatif (formules mathématiques).

2. DESCRIPTION DE L'ENVIRONNEMENT MODELSCREATOR

2.1. Principes de conception

2.1.1. Principes pédagogiques et cognitifs

     Le logiciel ModelsCreator est conçu de manière à constituer un environnement ouvert permettant à l'élève de travailler à plusieurs niveaux conceptuels (Dimitracopoulou et al., 1999). Créer lui-même des nouvelles situations - problèmes, procéder à la construction des modèles, c'est-à-dire choisir les entités, leurs propriétés et leurs relations, distinguer les représentations appropriées, etc. Sous cet aspect, l'élève est en mesure de comprendre la nécessité de la création des modèles dans les sciences et par conséquent les raisons pour lesquelles nous les inventons (interprétation des phénomènes, interprétation des données, prévision des résultats et des faits, etc.). Il est également en mesure d'acquérir des compétences de modélisation (s'interroger sur le problème, formuler des hypothèses, créer le modèle, contrôler le modèle, améliorer le modèle) et donc de construire des concepts, d'établir des relations, de découvrir des règles et des lois, de comprendre des théories (Komis et al., 1998).

     ModelsCreator permet la visualisation maximale d'entités, de propriétés et de valeurs, tenant compte du fait que la visualisation favorise à un degré important le développement du raisonnement chez les enfants (Teodoro, 1997).

2.1.2. Principes ergonomiques

     L'interface du ModelsCreator est basée sur la visualisation optique maximale des entités (représentant des idées ou des concepts) et des liens (représentant des relations mathématiques ou logiques). Les entités ont un "comportement" - dépendant de leurs propriétés - facilement simulé dans l'interface du logiciel par le biais de la manipulation directe sur laquelle est fondée toute l'interaction homme-ordinateur. L'environnement offre, à part la simulation réelle du modèle, d'autres représentations alternatives et multiples telles les diagrammes à barre, les représentations graphiques, les tables de valeurs, les tables de décision.

2.2. Architecture de l'environnement

     ModelsCreator est construit par une approche programmation objet (Ogborn, 1997) et il comporte cinq composantes principales (fig. 1) :

Figure 1 : L'interface du ModelsCreator présentant ses principales composantes.

1. L'espace des "situations - problèmes" contenant les problèmes à modéliser. Dans cet espace, on peut également créer de nouveaux problèmes. Un nouveau problème se construit dans l'éditeur des problèmes où l'on peut rédiger l'énoncé du problème et importer des éléments multimédias.

2. L'espace de la "construction et de l'exploration du modèle" qui contient la zone de visualisation du modèle en construction, les outils de construction et l'espace de l'exécution (simulation du comportement du modèle). Pour créer un modèle il faut préciser, à l'aide des outils de construction, les entités du modèle, les propriétés de chaque entité, les relations entre ces entités.

3. Le "dossier de notes" qui est à la disposition de l'élève pour prendre des notes pendant la construction et l'exécution du modèle. Il constitue par conséquent un outil métacognitif favorisant le développement de la métacognition (Vosniadou S. et al., 1994, Dimitracopoulou A.
   et al., 1997).

4. L'espace de collaboration comportant tous les outils spécifiques pour échanger facilement situations - problèmes et modèles en réseau local et sur Internet en mode synchrone.

5. L'"encyclopédie : modèles des sciences" qui est un hypermédia dont le thème concerne la modélisation dans les sciences et les différents secteurs scientifiques.

     Dans l'espace de la "construction et de l'exploration du modèle", l'élève peut choisir les objets du modèle, régler leurs propriétés et les lier avec des relations appropriées (selon sa représentation mentale du modèle). Ensuite, il peut le tester, le modifier et suivre son exécution sous plusieurs représentations multiples (simulation, diagramme à barres, graphique, tableau de valeurs, table de décision, etc.). Les objets se présentent sous une forme concrète (correspondant à l'objet lui-même et ayant un comportement proche à nos sens) ou abstraite (correspondant au concept à associer).

     Les relations disponibles sont classées en quatre grandes catégories :

1. Relations qualitatives logiques : pouvant être exprimées par des opérateurs logiques (et, ou, négation) et des structures de contrôle (si ... alors) très utiles pour la prise de décision.

2. Relations qualitatives d'ordre sémantique : constituant des liens utilisés dans la cartographie conceptuelle.

3. Relations semi-quantitatives : exprimant la variation des valeurs de propriétés des objets liés et la direction de cette variation de façon purement qualitative. Dans la version actuelle, l'élève peut utiliser des relations iconiques ( , , , or ) correspondant à des formules mathématiques courantes (proportionnalité, proportionnalité inverse, etc.), qui s'expriment comme : "si une entité augmente, l'autre augmente aussi, diminue, reste constante", etc.

4. Relations quantitatives de forme algébrique : exprimées par les opérateurs algébriques courants (+, -, *, /, =) et sont utilisées à l'aide d'une interface permettant de relier les propriétés d'un modèle construit dans l'espace de travail.

     Dans la partie suivante, nous analysons l'utilisation du ModelsCreator dans des situations-problèmes qui nécessitent l'utilisation des règles de logique et de prise de décision.

3. APPLICATION DU MODELSCREATOR DANS DES SITUATIONS DE LOGIQUE ET DE PRISE DE DÉCISION

3.1. Cadre théorique

     Le processus de construction de concepts de logique n'est en aucun cas une activité triviale, mais présente des difficultés toutes particulières. Étant une notion abstraite, la logique semble quelquefois avoir peu de rapport avec les problèmes réels du monde qui nous entoure (Fung et al., 1992, van der Pal, 1993). Les difficultés rencontrées par les élèves au niveau de la compréhension des notions et des règles de logique constituent un phénomène très fréquent. Même à l'issue d'un enseignement régulier en matière de logique, nombreux sont les élèves qui ne réussissent pas à appréhender les principes essentiels du raisonnement modal, dans le cas où ces principes ne seraient pas entièrement compris (Fung et al., 1992).

     Des conclusions logiques portant sur la réalité qui nous entoure peuvent parfois entrer en contradiction avec les considérations et les opinions des élèves (Dobson, 1994). D'une part, ceci mène souvent à la confusion et, d'autre part, empêche le progrès de la procédure logique, vu que "le caractère logique" de la conclusion est souvent "évalué" par rapport au degré de la mise en relation avec les considérations mêmes des élèves (Gill et al., 1994 ; Campbell, 1995). Ce genre de comportements des élèves est en général inconscient et dépend souvent du cadre général de la question étudiée ; ils se transforment difficilement, rendant de la sorte difficile la présentation d'exemples généralisés convaincants (White et al. ; 1991, Draper et al., 1992).

     Le caractère essentiel des processus de résolution de problèmes et de prise de décision est reconnu à divers niveaux (éducation, industrie, économie, politique, etc.). Le passage relativement récent à l'ère de l'informatique fait se concentrer l'intérêt sur les logiciels éducatifs, développant et renforçant la mise en valeur de compétences relatives aux processus susmentionnés. Il est considéré que les stratégies mises au point pendant ces processus devraient représenter un élément de première importance dans le cadre de l'enseignement contemporain. Bien qu'une convergence soit constatée au niveau des points de vue relatifs aux démarches urgentes, nécessaires pour le processus de résolution des problèmes, il existe néanmoins une divergence d'opinions en matière de techniques précises, nécessaires à chaque étape de ce processus (Huitt, 1992). Dans ce sens, la mise en place d'un logiciel éducatif de résolution de problèmes avec des règles de logique acquiert une importance particulière.

     La mise en valeur de la pensée logique et le développement des capacités de résolution de problèmes reflètent directement la possibilité de prise de décision. Le processus de la prise de décision se fonde sur les processus découlant de la logique et constitue une activité rencontrée à tous les niveaux de l'existence humaine, à tous les âges. Elle représente une compétence fondamentale de l'homme à importance et utilité multiple. Sa mise en valeur et sa consolidation contribuent au renforcement de la personnalité de l'individu.

     La complexité de l'enseignement de la prise de décision se situe à la compréhension et, par conséquent, à l'utilisation correcte des opérateurs logiques fondamentaux. L'approche de ces notions a lieu de façon limitée en ce qui concerne le collège [1]. Dans ce contexte, ModelsCreator propose une approche de la résolution de problèmes avec l'utilisation de connecteurs logiques par le moyen d'un environnement informatique spécialisé.

3.2. Aspects pédagogiques : prise de décision et règles de logique dans l'enseignement

     Le raisonnement qualitatif est une catégorie de raisonnement où s'inscrivent de nombreux problèmes de connaissance scolaire portant sur tous les thèmes qui ne peuvent pas être exprimés de façon algébrique. La plupart des problèmes que rencontre un jeune élève nécessitent une approche qualitative et non pas quantitative, ce qui rend la modélisation par le moyen d'un raisonnement qualitatif, un outil particulièrement utile.

     Dans la présente étude, nous sommes intéressés par le genre de raisonnement qualitatif qui survient pendant le processus de prise de décision. Cette question particulière est en relation immédiate avec les sujets enseignés dans le cadre des cours comme ceux d'Économie, d'Orientation Professionnelle Scolaire et d'Informatique, etc. La compétence de prise de décision constitue un principal objectif didactique, au moins pour ces cours. Cependant, la compétence de prise de décisions est un élément bien plus important qu'un simple objet cognitif. Le logiciel ModelsCreator vise à la mise en valeur et le développement de cette compétence chez les élèves.

     La question de la prise de décision, de la manière dont elle est présente dans les livres scolaires, ne facilite pas les élèves à l'appréhender correctement, étant donné que les traitements logiques qui devront être effectués pour la prise d'une décision ne sont ni mentionnés ni, bien sûr, analysés. La façon dont la question est présentée, ne rend pas aisée la compréhension de la part des élèves des mécanismes nécessaires, activés pendant une telle procédure.

     Les considérations actuelles de la psychologie de l'apprentissage préconisent une approche des divers objets cognitifs à travers des activités de résolution de problèmes (Vosniadou et al., 1994). Models Creator traite du processus de prise de décision à travers une approche de problèmes et leur modélisation, conformément aux problématiques contemporaines de la didactique et des sciences cognitives (Ogborn, 1990, Bliss et al., 1992, Mellar et al., 1994). Il fournit des représentations d'objets et de situations réelles en vue d'une vérification immédiate du modèle créé par l'élève, présentant en même temps les conséquences des situations qu'il a définies, tout en proposant parallèlement une table de décision comme forme alternative de représentation et de vérification simultanée.

     Le processus de prise de décision est en relation immédiate avec les règles de logique. Cependant, l'apprentissage n'est pas identifié à la simple mise en application des règles. L'approche adoptée par Models Creator vise à la mise en place des situations-problèmes auxquels les élèves sont appelés à faire face. La capacité de pouvoir évaluer une situation et d'agir avec lucidité quant à son évolution, constitue sans aucun doute une ressource et une aptitude cruciale pour l'élève. La capacité dans le processus de la prise de décision représente un avantage essentiel pour la personnalité de l'individu, renforce son efficacité, la confiance en soi, ses compétences administratives. Les compétences développées par les élèves pendant l'exercice de leur capacité dans ce domaine consolident le raisonnement qualitatif, le mode de raisonnement le plus complet et le plus important.

     L'utilisation de règles de logique présuppose l'utilisation de opérateurs logiques (ET, NON, SOIT) et de corrélations logiques (SI ... ALORS ...). La familiarisation des élèves des dernières classes du collège avec ces termes et notions est considérée comme expérience préalable très utile dans la perspective de leur contact avec le cours obligatoire ou optionnel de l'Informatique en Lycée, au cours duquel les élèves s'occuperont de façon plus exhaustive des structures de programmation et des règles de logique.

     La mise en relation des divers objets fournis à l'élève pour la réalisation du modèle se fait de façon qualitative, avec l'utilisation des opérateurs logiques et des corrélations logiques. En vue d'une mise en relief des décision logiques, ModelsCreator permet de multiples approches :

• Exploration, modification, extension, où les élèves étudient des modèles déjà prêts, correspondant à des situations-problèmes présentées.

• Expression, où les élèves sont appelés à modéliser les problèmes posés par eux-mêmes ou par d'autres personnes.

• Utilisation de la table de décision pour valider les situations-problèmes proposées par le logiciel ainsi que dans des situations de logique concernant de nouveaux problèmes ouverts.

3.3. Aspects didactiques et objectifs d'apprentissage

     La modélisation constitue une caractéristique intrinsèque de la recherche scientifique, mais également de l'acte éducatif (Ogborn, 1990). Il est à noter que dernièrement, à la suite de travaux en sciences cognitives et en didactique des sciences, plusieurs pays ont adopté l'introduction de la notion de modélisation au sein des programmes scolaires, comme par exemple en Grande Bretagne (National Curriculum) : "Pupils should be able to use information technology to design, develop, explore and evaluate models of real and imaginary situations" (http://www.nc.uk.net/home.html).

     Dans le cadre de sa culture générale, l'élève devra développer des compétences de modélisation. Des recherches effectuées dans le cadre de la didactique des sciences et de la psychologie cognitive mettent en évidence que l'application du processus de modélisation constitue en réalité un processus d'apprentissage pour l'élève-même, et ce pour diverses raisons (Beckett and Boohan, 1995 ; Ogborn, 1997) :

• À travers l'effort de conception de modèles, les élèves expriment leurs idées et leurs modèles mentaux. Cette expression est un premier pas dans la direction de la reconnaissance de leurs raisonnements.

• Les représentations graphiques et symboliques qui peuvent être attribuées aux modèles jouent un rôle de soutien du raisonnement, un rôle accompagnateur de la pensée.

• La mise en place et l'étude des modèles ont un rôle de renforcement, afin de faire des idées un objet de communication entre les élèves et leurs camarades de classe ou leurs professeurs.

Dans ce cadre, ModelsCreator a comme objectif d'aider les élèves à :

• Trouver la relation logique de diverses situations et de procéder à la prise de décision selon les valeurs de ces situations ;

• Étudier l'évolution dynamique des situations et résoudre des problèmes quotidiens qui nécessitent une prise de décision ;

• Avoir une approche intuitive des situations de la vie quotidienne avec une utilisation sous-jacente des opérateurs logiques et une représentation virtuelle du problème.

Les outils didactiques et cognitifs utilisés sont les suivants :

• Analyse et résolution des problèmes avec une utilisation sous-jacente des opérateurs logiques.

• Utilisation de la table de décision.

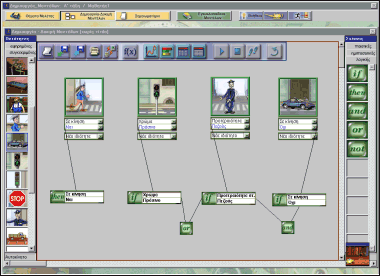
3.4. Prise de décision et modèles qualitatifs dans ModelsCreator

     Dans cette partie est présentée (à titre d'exemple) une situation-problème portant sur la Prise de décision et son approche didactique et pédagogique. Il faut noter que dans l'environnement ModelsCreator, et pour chaque unité thématique [2], il est conseillé que les élèves travaillent sur un scénario central qui dans le cas de la prise de décision a pour titre "La traversée".

     La formulation d'une situation-problème appartenant à ce scénario apparaît dans l'"Espace des situations-problèmes" : "Une personne se trouvant sur le trottoir désire passer de l'autre côté de la rue. Elle doit cependant faire attention à ce qu'elle ne soit pas écrasée par une voiture. Si tu te trouvais à sa place, quelles sont à ton avis les conditions nécessaires afin que tu puisses arriver en toute sécurité au trottoir d'en face ?"

     Dans cette situation-problème, ce qui est demandé c'est le comportement du piéton. Les élèves sont appelés à exprimer leur avis quant à la façon dont ils auraient réagi s'ils se trouvaient à la place du piéton. Toute conclusion tirée doit se rapporter au piéton et non pas à la voiture ou toute autre entité intervenant éventuellement dans la construction du modèle qu'ils sont appelés à créer. Par la suite, en essayant le modèle, ils peuvent procéder à la formulation de remarques relatives à la validité de son comportement et le comparer aux modèles respectifs de leurs camarades de classe.

Figure 2 : Un modèle de la "Traversé" dans ModelsCreator.

     Le scénario "La Traversée" a été choisi pour deux raisons différentes :

• Il offre aux élèves la possibilité de traiter d'une question qui leur est particulièrement familière, il s'inscrit donc dans une problématique de résolution des problèmes se référant au vécu des élèves.

• Il peut être étudié à travers la création de modèles qui adoptent la mise en application d'un raisonnement qualitatif.

     Les objectifs didactiques de ce scénario peuvent être définis comme suit : analyse et représentation de simples questions de la vie quotidienne, résolution de simples problèmes du quotidien nécessitant une prise de décision, utilisation sous-jacente des opérateurs logiques, rédaction d'une structure de sélection et constatation de la validité ou pas du mode de rédaction, utilisation de la table de décision.

3.4.1. Création d'un modèle

     D'après la description de la situation-problème, l'élève doit placer dans la composante "construction et de l'exploration du modèle" ; les entités qui sont requises pour traiter du problème. La manipulation directe d'une part, la minimalisation de la "distance d'exécution" d'autre part (O'Malley, 1990), c'est-à-dire la distance entre l'objectif de l'élève et les actions qu'il devra accomplir afin de l'atteindre, figurent parmi les principes fondamentaux de conception offerts par le logiciel. Dès qu'une entité est placée dans l'espace de création du modèle, l'élève peut lui attribuer une ou plusieurs propriétés. L'attribution d'une valeur initiale à une propriété est effectuée automatiquement par le logiciel. Si cette valeur ne correspond pas à la représentation de l'élève, celui-ci peut la modifier.

     L'action ultérieure de l'élève réside en la définition des liens logiques entre les propriétés des entités. Utilisant des liens logiques, il doit mettre en rapport approprié les propriétés qu'il a définies pour les entités qu'il a sélectionnées. Les liens logiques utilisés font partie des relations qualitatives de l'environnement de travail du logiciel. Plus précisément, les liens utilisés sont les suivants :

• la conjonction (ET),

• l'alternative (OU),

• la négation (NON),

• la supposition (SI),

• l'attribution ou la conclusion (ALORS).

     L'attribution de liens aux propriétés des entités ou à d'autres relations suit certaines règles et se soumet à certaines restrictions. Plus particulièrement :

• à chaque caractéristique ne peut être attribué qu'un seul lien,

• deux suppositions (SI) ou deux conclusions (ALORS) peuvent se relier seulement avec une conjonction (ET) ou une alternative (OU),

• la supposition (SI) et la conclusion (ALORS) ne peuvent pas être reliées,

• afin qu'un modèle de logique soit considéré complet et que l'élève puisse "l'exécuter" (c'est-à-dire l'essayer pour voir son comportement), il faut qu'au moins une supposition (SI) et au moins une conclusion (ALORS) soient définies.

3.4.2. Essai du modèle

     L'examen de la situation-problème par l'élève peut aboutir à la création du modèle. Celui-ci n'est pas l'unique modèle acceptable, d'autres modèles "alternatifs" pourraient être mis au point, également corrects et acceptables.

     Dès que l'élève accomplit la réalisation du modèle, il est ensuite en mesure de l'essayer. L'essai du modèle donne aux élèves l'occasion d'étudier son comportement et de tenter de l'améliorer. L'essai peut être effectué soit avec une exécution automatique soit avec une exécution progressive (par étapes ou pas à pas). Dans les deux cas, les touches respectives sont fournies par la commande de l'environnement du logiciel. Le comportement du logiciel dépend de ce qui a été repris dans le modèle, par exemple :

• il présente une simulation de traversée efficace de la rue par le piéton, si les propriétés des entités et des relations utilisées ont acquis les valeurs appropriées ;

• il présente une simulation d'accident du piéton avec une voiture, si les propriétés des entités et des relations utilisées ont acquis des valeurs "inappropriées" ;

• il ne présente aucune simulation dans une série de cas où le modèle proposé ne répond pas à la question posée par la question d'étude examinée.

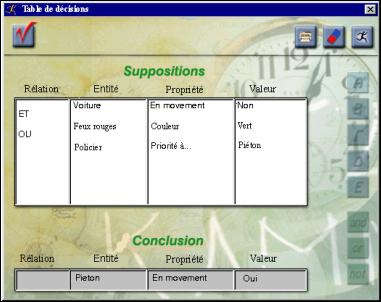
3.4.3. Utilisation de la table de décision

     La création de l'interface d'utilisateur de la table de décision, mais également du logiciel dans son ensemble, répond aux critères essentiels d'ergonomie (McGraw, 1992). Afin de permettre une compréhension plus approfondie des modèles d'ordre logique et de prise de décision, ModelsCreator propose, par le biais de sa table de décision (fig. 3), la possibilité d'une représentation alternative. La table de décision peut être utilisée de deux façons différentes :

• Contrôle de la validité du modèle. L'élève peut contrôler la validité du modèle qu'il a mis en place. La table de décision apparaît informée par le modèle mis en place par l'élève. Si l'élève modifie son modèle, à sa réouverture la table de décision reflétera les changements. En choisissant la touche de contrôle appropriée de la table de décision, l'élève peut contrôler la validité de son modèle. La table de décision donne aussi la possibilité à l'élève de changer les valeurs des propriétés des entités et de demander à nouveau un contrôle du modèle.

• Rédaction et étude des propositions logiques générales. La seconde manière d'utilisation de la table de décision est générale et attribue à cet "outil" du logiciel un caractère "ouvert". L'élève peut utiliser la table de décision pour la rédaction, l'étude et le contrôle de la validité de propositions logiques généralisées, en procédant aux étapes suivantes :

1. Il choisit une des cinq touches disponibles (A-E). Le nom de la touche est automatiquement enregistré dans la section Suppositions et dans la colonne Propriétés, alors que la valeur Oui est enregistrée dans la colonne Valeurs. Les (A-E) correspondent à des propositions logiques que l'élève peut considérer et qui peuvent recevoir les valeurs Oui, Non (vrai, faux).

2. Il choisit un des connecteurs logiques, conjonction (AND), alternative (OR), qui est automatiquement enregistré dans la colonne Lien.

3. Dans l'étape suivante, il choisit à nouveau une des touches restantes (A-E), qui est également enregistrée dans la colonne Propriétés et se voit attribuer la valeur Oui dans la colonne Valeurs. Les étapes (1) et (2) peuvent être répétées encore une fois à titre facultatif.

4. Par la suite, il choisit encore une des touches restantes dans la section Conclusion. Le nom de la touche (A-E) est automatiquement enregistré dans la section Suppositions et dans la colonne Propriétés, alors que dans la colonne Valeurs s'enregistre la valeur Oui.

5. S'il le considère nécessaire, l'élève modifie les valeurs automatiquement enregistrées et choisit la touche de contrôle pour constater le caractère correct ou erroné de son raisonnement.

     Il faut souligner aux élèves que l'inscription d'une proposition dans la partie Conclusion ne concerne pas une proposition indépendante, mais une combinaison logique de propositions et de relations enregistrées dans la partie Suppositions.

     Ce mode d'utilisation de la table de décision constitue une introduction des élèves à l'Algèbre Boole.

Figure 3 : La table de décision dans ModelsCreator

4. CONCLUSIONS ET PERSPECTIVES

     ModelsCreator peut être utilisé de deux manières générales, dans le cadre de la prise de décision :

• en tant qu'aide au programme scolaire, dans le cadre des besoins éducatifs de différents cours comme l'Économie et l'Informatique,

• en tant qu'élément à intégrer dans le cadre d'un effort plus général d'une révision substantielle et d'une amélioration du programme scolaire, fondées sur des activités interdisciplinaires.

     Dans ce sens, la rédaction de la structure de sélection (SI ... ALORS ...) au ModelsCreator se différencie par rapport à la rédaction de la même structure au niveau de l'algorithmique et des langages de programmation. Alors qu'en algorithmique et dans les langages de programmation, la supposition (SI) est utilisée une fois, pouvant être accompagnée de nombreuses conditions qui sont en relation et se combinent entre elles avec l'utilisation des opérateurs logiques (ET) soit (OU), de nombreuses suppositions (SI) sont utilisées dans l'environnement du ModelsCreator, entrant en relation avec les connecteurs (ET) soit (OU). Au cours d'une étude "clinique" concernant une évaluation formative du cycle d'implantation du logiciel, cette approche s'est avérée plus compréhensible pour les élèves, étant donné qu'il s'agit de la transposition exacte du discours oral le plus habituel des élèves, qui, souhaitant exprimer le besoin de satisfaction de la supposition, répètent à plusieurs reprises la supposition (SI).

     Des expérimentations déjà faites avec ModelsCreator sur des situations-problèmes en mathématiques en se servant des raisonnements semi-quantitatifs (Komis et al., 2001) ont donné des résultats intéressants concernant le processus de modélisation conduit par les élèves.

     Néanmoins, d'autres aspects devront être étudiés actuellement pour avoir une image complète de l'usage de l'environnement. Ces aspects concernent l'analyse des interactions élève(s) - professeur - environnement informatique, l'analyse détaillée du discours des élèves au cours du processus de modélisation et l'analyse des usages des représentations alternatives à une multitude de situations variées, afin d'étudier aussi les effets sur l'apprentissage des concepts impliqués, ainsi que sur le processus de modélisation lui-même.

Panagiotis POLITIS Maître de Conférences, Département de l'Éducation Technologique, Université de Pirée, 80, Karaoli-Dimitriou, 18534, Pirée, Grèce ppol@hol.gr

Vassilis KOMIS Maître de Conférences, Département de l'Éducation, Université de Patras 26500, Rion, Patras, Grèce komis@upatras.gr

Angélique DIMITRACOPOULOU Professeur Assistant, Département de l'Éducation, Université d'Egée, 1, Av. Demokratias, 85100, Rhodes, Grèce, adimitr@rhodes.aegean.gr

Remerciements : Le développement de la première version du Models Creator a été financé par le programme Seirines/Odyssée et la version en développement est financée par le programme Pénélope/Odyssée du Ministère de l'Éducation Hellénique.

BIBLIOGRAPHIE

Beckett, L. et Boohan, R. (1995). Computer Modelling for the Young -and not so Young - Scientist, Thinker, R. (éd), Microcomputer Based Labs : Educational Research and Standards, Springer Verlag, NATO ASI Series, 156, p. 227-238.

Bliss J., Ogborn J., Boohan R., Brosnan T., Brough D. et Mellar H. (1992). Tools for Exploratory Learning Program End of Award Review Report, London, University of London.

Bruillard É. (1996). Les machines à enseigner, Editions Hermès, Paris.

Campbell K., Collins K. et Watson J. (1995). Visual Processing During Mathematical Problem Solving, Educational Studies in Mathematics, (28), Netherlands, p. 177-194.

Dimitracopoulou A. et Komis V. (1999). Permettre aux élèves des activités multiples de modélisation et des approches interdisciplinaires à l'aide d'un nouveau environnement informatique, Actes des XXI journées internationales sur la communication, l'éducation et la culture scientifiques et techniques, Chamonix, p. 243-248.

Dimitracopoulou A., Komis V., Apostolopoulos P. et Politis P. (1999). Design principles of a new modelling environment for young students, supporting various types of reasoning and interdisciplinary approaches, in 9^th International Conference on Artificial Intelligence in Education, AI-ED 99, Le Mans, France, p.109-112.

Dimitracopoulou A., Vosniadou S. et Ioannides C. (1997). Exploring and Modeling the real world through designed environments for young children, In 7th European Conference for Research on Learning and Instruction, Athens, EARLI.

Dobson M. (1994). Towards an Analysis of Visual Media in Relation to Learning Outcomes : A Study in Improving Syllogistic Reasoning Skills, Institute of Educational Technology, UK, Open University.

Draper S., Mohammed R., Byard M., Driver R., Hartley R., Mallen C., Twigger D., O'Malley C., Hennesey S., O'Shea T., Scanlon E. et Spensley F. (1992). Conceptual Change in Science : Final Report to the ESRC, CALRG Technical Report 123, UK, Open University.

Ferber J. (1995). Les systèmes multi-agents, vers une intelligence collective, Paris, InterEditions, Paris.

Fung P. et O'Shea T. (1992). Learning to reason formally about programs : an observational study of Computer Science students, CITE report 168, UK, Open University.

Genzling J.-C. et Pierrard M.-A. (1994). La modélisation, la description, la conceptualisation, l'explication et la prédiction, in Nouveaux regards sur l'enseignement et l'apprentissage de la modélisation en sciences, Paris : INRP, Équipe INRP / LIREST.

Gill S. et Wright D. (1994). A Hypercard Based Environment for the Constructivist Teaching of Newtonian Physics, British Journal of Educational Technology, 25 (2), p.135-146.

Huitt W. (1992). Problem solving and decision making : Consideration of individual differences using the Myers-Briggs Type Indicator, Journal of Psychological Type, 24, p. 33-44.

Komis V., Dimitracopoulou A. et Politis, P. (1988). Contribution à la conception et au développement d'un environnement de modélisation, Rouet, J.-F. et De La Passardière D. (éds), in Quatrième colloque Hypermédias et Apprentissage, Poitiers, EPI-INRP, p. 263-268.

Komis V., Dimitracopoulou A., Politis P. et Avouris N. (2001). Expérimentations sur l'utilisation d'un logiciel de modélisation par petits groupes d'élèves, 6^èmes Journées d'Environnements Interactifs d'Apprentissage, Paris, HERMES.

McGraw K. (1992). Designing and Evaluating User Interfaces for Knowledge_based Systems, West Sussex, England, Ellis Horwood Limite.

Mellar H., Bliss J., Boohan R., Ogborn J. et Tompsett (éds) (1994). Learning with Artificial Worlds : Computer Based Modelling in the Curriculum, London, The Falmer Press.

O' Malley C. (1990). Interfaces issues for guided discovery environments, in Elsom-Cook M. (Ed.) Guided Discovery Tutoring : A framework for ICAI Research, London, Paul Chapman Publishing Ltd.

Ogborn J. (1990). A future for modelling in science education, Journal of Computer Assisted Education, Oxford, Blackwell Scientific.

Ogborn J. (1997). "WordMaker" : Design Principles for an Object Oriented Modelling System accessible to Young Pupils", in 7th European Conference for Research on Learning and Instruction, Athens, EARLI.

Papert S. (1980). Mind-Storms, Children, Computers and Powerful Ideas, New York, Basic Books.

Soloway E., Shari L. et Jaskson S. (1996). Learning Theory in Practice : Case Studies of learner- Centered Design, in CHI 96 Conference Proceedings. Human Factors in Computing Systems, Vancouver, p. 189-196.

Teodoro V.D. (1994). Learning with Computer-Based Exploratory Environments in Science and Mathematics, in S. Vosniadou, E. De Corte, H. Mandl (éds.), Technology -Based Learning Environments : Psychological and Educational Foundations, NATO ASI Series , Série F : Computer and Systems Sciences,137, Berlin : Springer Verlag, p. 179-186.

Teodoro V.D. (1997). Modellus : Using a Computational Tool to Change the Teaching and Learning of Mathematics and Science, Paper presented at the UNESCO Colloquium "New Technologies and the Role of the Teacher", UK, Open University, Milton Keynes.

Van Der Pal J. (1993). Formal Conditional Reasoning : Does Graphical Instruction Enhance Learning Outcome ? Proceedings of the AI-ED93 Workshop on Graphical Representations, Raisoning and Communication, Edinburgh, p. 28-32.

Vosniadou S., De Corte E. et Mandl H. (1994). Technology-Based Learning Environments (éd), Spinger Verlag, 137.

Webb M., (1995). Computer-based modelling in school science, in SCR - 1993, p. 33-44.

White B. et Horwitz P. (1991). Computer Microwords and Conceptual Change : A New Approach to Science Education, in O. Boyd-Barett and E. Scanlon (éds), Computers and Learning, Wokingham, Addison Wesley.

Paru dans la  Revue de l'EPI  n° 102 de juin 2001.

NOTES

[1] Par exemple, dans le système scolaire grec, la notion de la prise de décision est enseignée dans le cadre des cours d'Économie en 2^ème année du collège, d'Orientation Professionnelle Scolaire et d'Informatique en 3^ème année du collège.

[2] En version actuelle, il existe cinq grandes unités thématiques : mathématiques, physique, éducation à l'environnement, prise de décision, informatique.

___________________
(14 juin 2001)

Sommaires des Revues